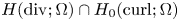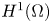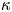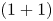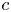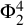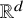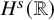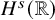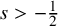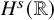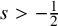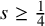Refine listing
Actions for selected content:
363 results in 35Qxx
Spectral asymptotics for linear elasticity: the case of mixed boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Opinion formation on evolving network: the DPA method applied to a nonlocal cross-diffusion PDE-ODE system
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 21 May 2024, pp. 748-775
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A global higher regularity result for the static relaxed micromorphic model on smooth domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-15
-
- Article
- Export citation
Unified framework for the separation property in binary phase-segregation processes with singular entropy densities
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 09 May 2024, pp. 40-67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bifurcation of the travelling wave solutions in a perturbed (1 + 1)-dimensional dispersive long wave equation via a geometric approach
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 April 2024, pp. 1-28
-
- Article
- Export citation
Modelling of the fluid flow in a thin domain with injection through permeable boundary
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 25 April 2024, pp. 776-796
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Macroscopic limit of a Fokker-Planck model of swarming rigid bodies
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 19 April 2024, pp. 349-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A remark on Gibbs measures with log-correlated Gaussian fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 April 2024, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Consensus-based optimisation with truncated noise
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 05 April 2024, pp. 292-315
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp well-posedness for the cubic NLS and mKdV in
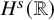 $H^s({{\mathbb {R}}})$
$H^s({{\mathbb {R}}})$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the reconstruction of unknown driving forces from low-mode observations in the 2D Navier–Stokes equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 01 April 2024, pp. 2171-2194
- Print publication:
- December 2025
-
- Article
- Export citation
Necessary and sufficient conditions for ground state solutions to planar Kirchhoff-type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1938-1959
- Print publication:
- October 2025
-
- Article
- Export citation
Dispersive and Strichartz estimates for 3D wave equation with a Laguerre potential
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 07 March 2024, pp. 863-890
- Print publication:
- June 2025
-
- Article
- Export citation
Derivation and travelling wave analysis of phenotype-structured haptotaxis models of cancer invasion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 27 February 2024, pp. 231-263
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A collision result for both non-Newtonian and heat conducting Newtonian compressible fluids
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1631-1645
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A data-driven kinetic model for opinion dynamics with social network contacts
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 20 February 2024, pp. 264-290
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
From NeurODEs to AutoencODEs: A mean-field control framework for width-varying neural networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 08 February 2024, pp. 188-230
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Network-based kinetic models: Emergence of a statistical description of the graph topology
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 02 February 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global dynamics and spatiotemporal heterogeneity of a preytaxis model with prey-induced acceleration
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 26 January 2024, pp. 601-633
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Trend to equilibrium solution for the discrete Safronov–Dubovskiĭ aggregation equation with forcing
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 16 November 2023, pp. 869-892
- Print publication:
- June 2025
-
- Article
- Export citation