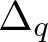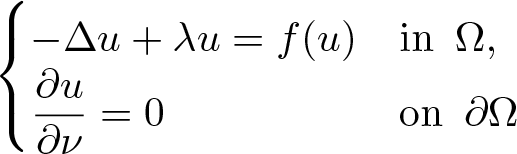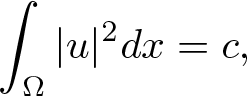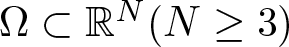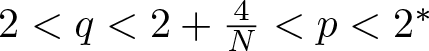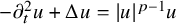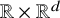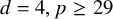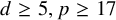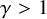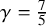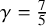Refine listing
Actions for selected content:
363 results in 35Qxx
Derivation of the Gross-Pitaevskii dynamics through renormalized excitation number operators
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 July 2025, e107
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global boundedness and stabilization of solutions for a chemotaxis system with acceleration and logistic source
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-30
-
- Article
- Export citation
Regularity criteria for the 3D Navier–Stokes and MHD equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 26 June 2025, pp. 1262-1296
-
- Article
- Export citation
A multiscale model for espresso brewing: Asymptotic analysis and numerical simulation
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 27 May 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cahn–Hilliard equations with singular potential, reaction term and pure phase initial datum
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 27 May 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the long-time asymptotics of the modified Camassa–Holm equation with step-like initial data
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 23 April 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal transport on gas networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 16 April 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Remark on the local well-posedness for NLS with the modulated dispersion
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-12
-
- Article
- Export citation
Numerical solution of a PDE arising from prediction with expert advice
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Solutions with prescribed mass for L2-supercritical NLS equations under Neumann boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On blow-up for the supercritical defocusing nonlinear wave equation
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 31 March 2025, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
3D Navier–Stokes–Voigt equations with damping and double delays on unbounded domains: Well-posedness, pullback attractors, and limit measures
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 March 2025, pp. 1-39
-
- Article
- Export citation
Rigorous derivation of a binary-ternary Boltzmann equation for a non ideal gas of hard spheres
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 March 2025, e52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unique compact representation of magnetic fields using truncated solid harmonic expansions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 1012-1039
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Well-posedness for the 3-D generalized micropolar system in critical Fourier–Besov–Morrey spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 26 February 2025, pp. 891-907
- Print publication:
- September 2025
-
- Article
- Export citation
Global well-posedness and Turing–Hopf bifurcation of prey-taxis systems with hunting cooperation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1121-1147
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A sharp threshold for Trudinger–Moser type inequalities with logarithmic kernels in dimension N
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-39
-
- Article
- Export citation
Smooth imploding solutions for 3D compressible fluids
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spatio-temporal behaviour of SIR models with cross-diffusion and vital dynamics
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 972-992
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
OPTIMAL CONTROL PROBLEMS GOVERNED BY MARGUERRE–VON KÁRMÁN EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 01 January 2025, e38
-
- Article
- Export citation