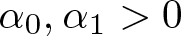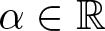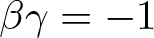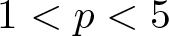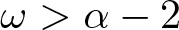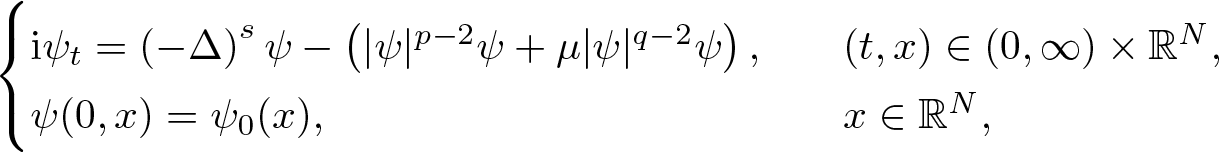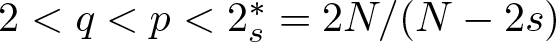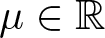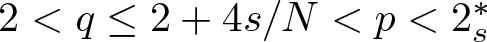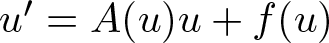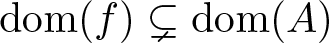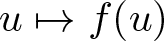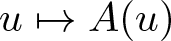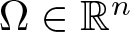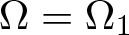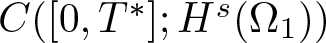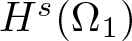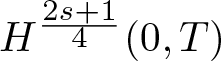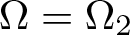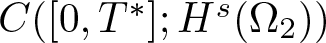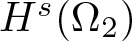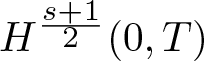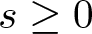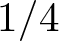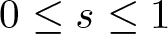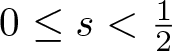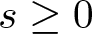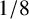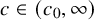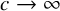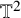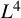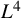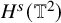Refine listing
Actions for selected content:
363 results in 35Qxx
NONRELATIVISTIC LIMIT FOR THE TRAVELLING WAVES OF THE PSEUDORELATIVISTIC HARTREE EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 26 December 2024, pp. 172-183
- Print publication:
- August 2025
-
- Article
- Export citation
Fractional time differential equations as a singular limit of the Kobayashi–Warren–Carter system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 December 2024, pp. 1-37
-
- Article
- Export citation
SYMMETRY RESTORATION IN COLLISIONS OF SOLITONS IN FRACTIONAL COUPLERS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 03 December 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral stability of constrained solitary waves for a generalized Ostrovsky equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2024, pp. 1-32
-
- Article
- Export citation
Stability conditions for mean-field limiting vorticities of the Ginzburg-Landau equations in 2D
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 27 November 2024, pp. 2029-2060
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Instability of standing waves for fractional NLS with combined nonlinearities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 November 2024, pp. 1-29
-
- Article
- Export citation
Well-posedness of quasilinear parabolic equations in time-weighted spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-33
-
- Article
- Export citation
On Riemann–Hilbert problem and multiple high-order pole solutions to the cubic Camassa–Holm equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-51
-
- Article
- Export citation
Radial solutions of initial boundary value problems of nonlinear Schrödinger equations in ℝn
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A remark on the well-posedness of the modified KdV equation in L2
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-26
-
- Article
- Export citation
Global existence of a weak solution for a reaction–diffusion system in a porous medium with membrane conditions and mass control
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 20 November 2024, pp. 2006-2028
- Print publication:
- December 2025
-
- Article
- Export citation
FURTHER ACCURACY VERIFICATION OF A 2D ADAPTIVE MESH REFINEMENT METHOD USING STEADY FLOW PAST A SQUARE CYLINDER
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 19 November 2024, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamical behaviour of a logarithmically sensitive chemotaxis model under time-dependent boundary conditions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 04 November 2024, pp. 638-664
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The evolution problem for the 1D nonlocal Fisher-KPP equation with a top hat kernel. Part 1. The Cauchy problem on the real line
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 25 October 2024, pp. 775-810
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Blowup of cylindrically symmetric solutions for biharmonic NLS
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 03 October 2024, pp. 1085-1098
-
- Article
- Export citation
Non-linear biphasic mixture model: Existence and uniqueness results
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 161-185
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a supersonic-sonic patch arising from the two-dimensional Riemann problem of the compressible Euler equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-40
-
- Article
- Export citation
Stabilization in a chemotaxis system modelling T-cell dynamics with simultaneous production and consumption of signals
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 570-583
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Axisymmetric Incompressible Viscous Plasmas: Global Well-Posedness and Asymptotics
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 September 2024, e79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strichartz estimates and global well-posedness of the cubic NLS on
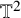 $\mathbb {T}^{2}$
$\mathbb {T}^{2}$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 09 September 2024, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation