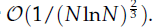Refine listing
Actions for selected content:
363 results in 35Qxx
An almost-periodic solution of Hasegawa–Wakatani equations with vanishing resistivity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 23 June 2016, pp. 983-1003
- Print publication:
- October 2016
-
- Article
- Export citation
A Posteriori Error Estimates for Conservative Local Discontinuous GalerkinMethods for the Generalized Korteweg-de Vries Equation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 22 June 2016, pp. 250-278
- Print publication:
- July 2016
-
- Article
- Export citation
Integrable Couplings of the Boiti-Pempinelli-Tu Hierarchy and Their Hamiltonian Structures
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 27 May 2016, pp. 588-598
- Print publication:
- August 2016
-
- Article
- Export citation
Parameter-Free Time Adaptivity Based on Energy Evolution for the Cahn-Hilliard Equation
- Part of
- Partial differential equations, boundary value problems
- Equations of mathematical physics and other areas of application
- Partial differential equations, initial value and time-dependent initial-boundary value problems
- Miscellaneous topics - Partial differential equations
- Elliptic equations and systems
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1542-1563
- Print publication:
- May 2016
-
- Article
- Export citation
On Fully Decoupled, Convergent Schemes for Diffuse Interface Models for Two-Phase Flow with General Mass Densities
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1473-1502
- Print publication:
- May 2016
-
- Article
- Export citation
Near-field Imaging Point-like Scatterers and Extended Elastic Solid in a Fluid
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1317-1342
- Print publication:
- May 2016
-
- Article
- Export citation
Accurate and Efficient Numerical Methods for Computing Ground States and Dynamics of Dipolar Bose-Einstein Condensates via the Nonuniform FFT
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1141-1166
- Print publication:
- May 2016
-
- Article
- Export citation
Entropy Stable Scheme on Two-Dimensional Unstructured Grids for Euler Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1111-1140
- Print publication:
- May 2016
-
- Article
- Export citation
A Numerical Study of Complex Reconstruction in Inverse Elastic Scattering
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1265-1286
- Print publication:
- May 2016
-
- Article
- Export citation
Solving Maxwell's Equation in Meta-Materials by a CG-DG Method
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1242-1264
- Print publication:
- May 2016
-
- Article
- Export citation
Novel Symplectic Discrete Singular Convolution Method for Hamiltonian PDEs
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1375-1396
- Print publication:
- May 2016
-
- Article
- Export citation
On Invariant-Preserving Finite Difference Schemes for the Camassa-Holm Equation and the Two-Component Camassa-Holm System
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 12 April 2016, pp. 1015-1041
- Print publication:
- April 2016
-
- Article
- Export citation
Pseudo-Arclength Continuation Algorithms for Binary Rydberg-Dressed Bose-Einstein Condensates
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 12 April 2016, pp. 1067-1093
- Print publication:
- April 2016
-
- Article
- Export citation
A Computational Study of a Data Assimilation Algorithm for the Two-dimensional Navier-Stokes Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 12 April 2016, pp. 1094-1110
- Print publication:
- April 2016
-
- Article
- Export citation
Efficient Implementation of Smoothed Particle Hydrodynamics (SPH) with Plane Sweep Algorithm
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 770-800
- Print publication:
- March 2016
-
- Article
- Export citation
An Adaptive Finite Element Method with Hybrid Basis for Singularly Perturbed Nonlinear Eigenvalue Problems
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 01 February 2016, pp. 442-472
- Print publication:
- February 2016
-
- Article
- Export citation
A Two-Level Method for Pressure Projection Stabilized P1 Nonconforming Approximation of the Semi-Linear Elliptic Equations
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 27 January 2016, pp. 386-398
- Print publication:
- June 2016
-
- Article
- Export citation
Exact Solutions for Fractional Differential-Difference Equations by (G'/G)-Expansion Method with Modified Riemann-Liouville Derivative
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 27 January 2016, pp. 293-305
- Print publication:
- April 2016
-
- Article
- Export citation
Mathematical Models for the Propagation of Stress Waves in Elastic Rods: Exact Solutions and Numerical Simulation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 27 January 2016, pp. 257-270
- Print publication:
- April 2016
-
- Article
- Export citation
SPECTRAL THEORETIC CHARACTERIZATION OF THE MASSLESS DIRAC ACTION
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 08 March 2016, pp. 701-718
- Print publication:
- 2016
-
- Article
-
- You have access
- Open access
- Export citation
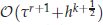 are obtained when polynomials of degree at most
are obtained when polynomials of degree at most 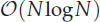 neighbour search method based on the plane sweep (PW) algorithm with
neighbour search method based on the plane sweep (PW) algorithm with