This paper considers estimators of parameters of the Boolean model which are obtained by means of the method of intensities. For an estimator of the intensity of the point process of germ points the asymptotic normality is proved and the corresponding variance is given. The theory is based on a study of second-order characteristics of the point process of lower-positive tangent points of the Boolean model. An estimator of the distribution of a typical grain is also discussed.

A random triangle in the plane is constructed using three independent elements from a convex set of lines. Expressions are given to calculate the shape distribution from the internal width function of the line set. Two examples are given together with their maximum angle distributions; a simple inequality implies a zero collinearity constant in general. A relationship between the shape distribution and inter-line angle distribution is given.

Consider a forest of maple trees in autumn, with leaves falling on the ground. Those coming late cover the others below, so eventually the fallen leaves form a statistically homogeneous spatial pattern. In particular, the uncovered leaf boundaries form a mosaic. We formulate a mathematical model to describe this mosaic, firstly in the case where the leaves are polygonal and later for leaves with curved boundaries. Mean values of certain statistics of the mosaic are derived.

Unbiased stereological estimators of d-dimensional volume in ℝn are derived, based on information from an isotropic random r-slice through a specified point. The content of the slice can be subsampled by means of a spatial grid. The estimators depend only on spatial distances. As a fundamental lemma, an explicit formula for the probability that an isotropic random r-slice in ℝn through O hits a fixed point in ℝn is given.

When a random electrical network has the structure of a rooted tree and the edge resistances are either inverse Gaussian or reciprocal inverse Gaussian random variables then, subject to some restrictions, the overall resistance of the network is shown to follow a reciprocal inverse Gaussian distribution.

This paper discusses a simple extension of the classical Voronoi tessellation. Instead of using the Euclidean distance to decide the domains corresponding to the cell centers, another translation-invariant distance is used. The resulting tessellation is a scaled version of the usual Voronoi tessellation. Formulas for the mean characteristics (e.g. mean perimeter, surface and volume) of the cells are provided in the case of cell centers from a homogeneous Poisson process. The resulting tessellation is stationary and ergodic but not isotropic.

This article investigates the accuracy of approximations for the distribution of ordered m-spacings for i.i.d. uniform observations in the interval (0, 1). Several Poisson approximations and a compound Poisson approximation are studied. The result of a simulation study is included to assess the accuracy of these approximations. A numerical procedure for evaluating the moments of the ordered m-spacings is developed and evaluated for the most accurate approximation.

The accuracy of the Poisson approximation to the distribution of the numbers of large and small m-spacings, when n points are placed at random on the circle, was analysed using the Stein–Chen method in Barbour et al. (1992b). The Poisson approximation for m≧2 was found not to be as good as for 1-spacings. In this paper, rates of approximation of these distributions to suitable compound Poisson distributions are worked out, using the CP–Stein–Chen method and an appropriate coupling argument. The rates are better than for Poisson approximation for m≧2, and are of order O((log n)2/n) for large m-spacings and of order O(1/n) for small m-spacings, for any fixed m≧2, if the expected number of spacings is held constant as n → ∞.

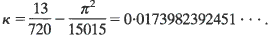
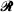Let denote a rectangular lattice in the Euclidean plane E 2, generated by (a × b) rectangles. In this paper we consider the probability that a random ellipse having main axes of length 2α and 2ß, with intersects . We regard the lattice 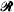as the union of two orthogonal sets 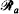and 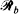of equidistant lines and evaluate the probability that the random ellipse intersects 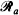or 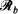. Moreover, we consider the dependence structure of the events that the ellipse intersects 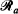or 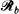. We study further the case when the main axes of the ellipse are parallel to the lines of the lattice and satisfy 2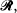ß = min (a, b) < 2α = max (a, b). In this case, the probability of intersection is 1, and there exist almost surely two perpendicular segments in within the ellipse. We evaluate the distribution function, density, mean and variance of the length of these segments. We conclude with a generalization of this problem in three dimensions.

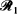Consider a compact body E embedded in a convex compact body G. A point P is randomly chosen in E and three different rays to the boundary ∂G of G are generated by P. Ray is in a uniformly random direction and has length 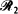R, ray is through a second random point chosen from within 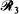G and has length W, and ray is to a random point in ∂G and has length Y. The distribution of Y is obtained and is related to previous work. When E is specialized to G or to ∂G, other known results are retrieved. The paper ends with a discussion of a conjecture relating the means of R, W and Y.

We analyze a class of stochastic and dynamic vehicle routing problems in which demands arrive randomly over time and the objective is minimizing waiting time. In our previous work ([6], [7]), we analyzed this problem for the case of uniformly distributed demand locations and Poisson arrivals. In this paper, using quite different techniques, we are able to extend our results to the more realistic case where demand locations have an arbitrary continuous distribution and arrivals follow only a general renewal process. Further, we improve significantly the best known lower bounds for this class of problems and construct policies that are provably within a small constant factor relative to the optimal solution. We show that the leading behavior of the optimal system time has a particularly simple form that offers important structural insight into the behavior of the system. Moreover, by distinguishing two classes of policies our analysis shows an interesting dependence of the system performance on the demand distribution.

This paper considers the histogram of unit cell size built up from m independent observations on a Poisson (μ) distribution. The following question is addressed: what is the limiting probability of the event that there are no unoccupied cells lying to the left of occupied cells of the histogram? It is shown that the probability of there being no such isolated empty cells (or isolated finite groups of empty cells) tends to unity as the number m of observations tends to infinity, but that the corresponding almost sure convergence fails. Moreover this probability does not tend to unity when the Poisson distribution is replaced by the negative binomial distribution arising when μ is randomized by a gamma distribution. The relevance to empirical Bayes statistical methods is discussed.

It is shown that the convex polygons are uniquely determined (up to translation and reflection) by their covariograms. The covariogram can be represented by the ‘orientation-dependent chord length distribution', i.e. the distribution of the length of chords which are generated by random lines parallel to fixed directions. Thus the result contributes to answer Blaschke's question about the content of information comprised in chord length distributions.

We obtain the distribution of the length of a clump in a coverage process where the first line segment of a clump has a distribution that differs from the remaining segments of the clump. This result allows us to provide the distribution of the busy period in an M/G/∞ queueing system with exceptional first service, and applications are considered. The result also provides the tool necessary to analyze the transient behavior of an ordinary coverage process, namely the depletion time of the ordinary M/G/∞ system.

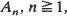Let , be i.i.d. random closed sets in 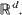. Limit theorems for their normalized convex hulls 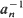conv (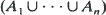) are proved. The limiting distributions correspond to 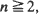C-stable random sets. The random closed set A is called C-stable if, for any , the sets 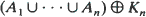anA and conv ( coincide in distribution for certain positive an, compact Kn , and independent copies A 1, …, An of A. The distributions of C-stable sets are characterized via corresponding containment functionals.

While the convex hull of n d-dimensional balls is not a polytope, it does have an underlying combinatorial structure similar to that of a polytope. In the worst case, its combinatorial complexity can be of order Ω(n [d/2]). The thrust of this work is to show that its complexity is typically much smaller, and that it can therefore be constructed more quickly on average than in the worst case. To this end, four models of the random d-ball are developed, and the expected combinatorial complexity of the convex hull of n independent random d-balls is investigated for each. As n grows without bound, these expectations are O(1), O(n (d–1)/(d+4)), O(1) (for d = 2 only), and O(n (d–1)/(d+3)).

A unified exposition of random Johnson–Mehl tessellations in d-dimensional Euclidean space is presented. In particular, Johnson-Mehl tessellations generated by time-inhomogeneous Poisson processes and nucleation-exclusion models are studied. The ‘practical' cases d = 2 and d = 3 are discussed in detail. Several new results are established, including first- and second-order moments of various characteristics for both Johnson–Mehl tesselations and sectional Johnson–Mehl tessellations.

This paper considers sets of points from a Poisson process in the plane, chosen to be close together, and their properties. In particular, the perimeter of the convex hull of such a point set is investigated. A number of different models for the selection of such points are considered, including a simple nearest-neighbour model. Extensions to marked processes and applications to modelling animal territories are discussed.

This paper presents the form of some characteristics of the Voronoi tessellation which is generated by a stationary Poisson process in . Expressions are given for the spherical and linear contact distribution functions. These formulae lead to numerically tractable double-integral formulae for chord length probability density functions.

Consider two convex bodies K, K′ in Euclidean space En and paint subsets β, β′ on the boundaries of K and K′. Now assume that K′ undergoes random motion in such a way that it touches K.