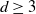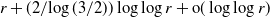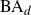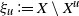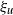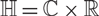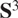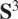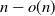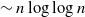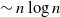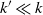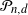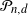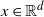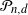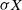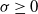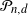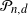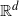Refine listing
Actions for selected content:
423 results in 60Dxx
Normal Approximation for Functions of Hidden Markov Models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 536-569
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
Cover time for branching random walks on regular trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 09 February 2022, pp. 256-277
- Print publication:
- March 2022
-
- Article
- Export citation
Intersections of random sets
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 17 January 2022, pp. 131-151
- Print publication:
- March 2022
-
- Article
- Export citation
On point processes defined by angular conditions on Delaunay neighbors in the Poisson–Voronoi Tessellation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 952-965
- Print publication:
- December 2021
-
- Article
- Export citation
On spatial matchings: The first-in-first-match case
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 757-800
- Print publication:
- September 2021
-
- Article
- Export citation
Random fractals and their intersection with winning sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 07 July 2021, pp. 655-684
- Print publication:
- May 2022
-
- Article
- Export citation
Continuum line-of-sight percolation on Poisson–Voronoi tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 July 2021, pp. 510-536
- Print publication:
- June 2021
-
- Article
- Export citation
Couplings for determinantal point processes and their reduced Palm distributions with a view to quantifying repulsiveness
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 469-483
- Print publication:
- June 2021
-
- Article
- Export citation
Projections of Poisson cut-outs in the Heisenberg group and the visual 3-sphere
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 March 2021, pp. 197-230
- Print publication:
- January 2022
-
- Article
- Export citation
Functional limit theorems for the euler characteristic process in the critical regime
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 March 2021, pp. 57-80
- Print publication:
- March 2021
-
- Article
- Export citation
Tail asymptotics of an infinitely divisible space-time model with convolution equivalent Lévy measure
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 42-67
- Print publication:
- March 2021
-
- Article
- Export citation
Existence of Gibbs point processes with stable infinite range interaction
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 775-791
- Print publication:
- September 2020
-
- Article
- Export citation
Decorrelation of a class of Gibbs particle processes and asymptotic properties of U-statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 928-955
- Print publication:
- September 2020
-
- Article
- Export citation
Breaking bivariate records
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 18 August 2020, pp. 105-123
-
- Article
- Export citation
A new approach to weak convergence of random cones and polytopes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 11 August 2020, pp. 1627-1647
- Print publication:
- December 2021
-
- Article
- Export citation
Randomized near-neighbor graphs, giant components and applications in data science
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 458-476
- Print publication:
- June 2020
-
- Article
- Export citation
Limit theory for unbiased and consistent estimators of statistics of random tessellations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 679-702
- Print publication:
- June 2020
-
- Article
- Export citation
Absorption probabilities for Gaussian polytopes and regular spherical simplices
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 588-616
- Print publication:
- June 2020
-
- Article
- Export citation
Asymptotic properties of random Voronoi cells with arbitrary underlying density
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 655-680
- Print publication:
- June 2020
-
- Article
- Export citation
Limit theorems for process-level Betti numbers for sparse and critical regimes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 29 April 2020, pp. 1-31
- Print publication:
- March 2020
-
- Article
- Export citation