Refine listing
Actions for selected content:
423 results in 60Dxx
Return to the Poissonian city
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 297-309
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Percolation on stationary tessellations: models, mean values, and second-order structure
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 311-332
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
On Random Disc Polygons in Smooth Convex Discs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 899-918
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Continuum AB percolation and AB random geometric graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 333-344
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Percolation on the Information-Theoretically Secure Signal to Interference Ratio Graph
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 910-920
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Size distributions in random triangles
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 283-295
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
On the Volume of the Zero Cell of a Class of Isotropic Poisson Hyperplane Tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 622-642
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Random Symmetrizations of Convex Bodies
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 603-621
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Invariant Bipartite Random Graphs on Rd
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 769-779
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
A Cellular Network Model with Ginibre Configured Base Stations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 832-845
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Stit Tessellations have Trivial Tail σ-Algebra
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 643-660
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
The Asymptotic Size of the Largest Component in Random Geometric Graphs with Some Applications
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 307-324
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Moments and Central Limit Theorems for Some Multivariate Poisson Functionals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 348-364
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
EXPECTED TOPOLOGY OF RANDOM REAL ALGEBRAIC SUBMANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 12 May 2014, pp. 673-702
- Print publication:
- October 2015
-
- Article
- Export citation
Local Digital Estimators of Intrinsic Volumes for Boolean Models and in the Design-Based Setting
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 35-58
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
On Comparison of Clustering Properties of Point Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 1-20
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
Semi-Infinite Paths of the Two-Dimensional Radial Spanning Tree
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 895-916
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Exact Formulae for Variances of Functionals of Convex Hulls
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 917-924
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Wicksell's Problem in Local Stereology
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 925-944
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Sliced Inverse Regression and Independence in Random Marked Sets with Covariates
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 626-644
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
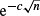 with
with 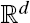 .
.


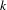
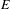
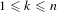
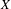
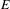

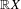
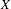

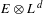
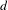
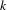

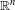
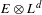


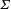
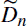 . These formulae are in line with asymptotic distribution results in Groeneboom (1988), Nagaev and Khamdamov (1991), and Groeneboom (2012), as well as with recent results in Pardon (2011), (2012).
. These formulae are in line with asymptotic distribution results in Groeneboom (1988), Nagaev and Khamdamov (1991), and Groeneboom (2012), as well as with recent results in Pardon (2011), (2012).