Refine listing
Actions for selected content:
423 results in 60Dxx
Excursion sets of three classes of stable random fields
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 293-318
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
On the induced distribution of the shape of the projection of a randomly rotated configuration
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 331-346
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
New Classes of Random Tessellations Arising from Iterative Division of Cells
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 26-47
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Sentry Selection in Wireless Networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-25
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Contact and Chord Length Distribution Functions of the Poisson-Voronoi Tessellation in High Dimensions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 48-68
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
RANDOM SUBSETS OF SELF-AFFINE FRACTALS
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 61-76
- Print publication:
- January 2010
-
- Article
- Export citation
Gamma distributions for stationary Poisson flat processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 911-939
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
On the expected maximum degree of Gabriel and Yao graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1123-1140
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Refined convergence for the Boolean model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 940-957
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Maximum likelihood estimation for cooperative sequential adsorption
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 978-1001
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Weighted faces of Poisson hyperplane tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 682-694
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
The existence of quermass-interaction processes for nonlocally stable interaction and nonbounded convex grains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 664-681
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
The chord length distribution function for regular polygons
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 358-366
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Nonparametric estimation of boundary measures and related functionals: asymptotic results
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 311-322
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Nearest-neighbor graphs on the cantor set
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 38-62
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Volume degeneracy of the typical cell and the chord length distribution for Poisson-Voronoi tessellations in high dimensions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 919-938
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Random Laguerre tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 630-650
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Lévy-based Cox point processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 603-629
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Monte Carlo methods for sensitivity analysis of Poisson-driven stochastic systems, and applications
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 293-320
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
Power diagrams and interaction processes for unions of discs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 321-347
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
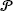 be a Poisson process of intensity one in the infinite plane ℝ
be a Poisson process of intensity one in the infinite plane ℝ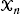 be a collection of
be a collection of 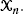 We prove convergence to a constant of the rescaled expected total edge length of this random graph. The rescaling factor is a function of the fractal dimension and has a log-periodic, nonconstant behavior.
We prove convergence to a constant of the rescaled expected total edge length of this random graph. The rescaling factor is a function of the fractal dimension and has a log-periodic, nonconstant behavior.