Refine listing
Actions for selected content:
423 results in 60Dxx
Estimation of the mean normal measure from flat sections
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 31-48
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
The iteration of random tessellations and a construction of a homogeneous process of cell divisions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 49-59
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
The Necklace Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 271-278
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Short-length routes in low-cost networks via Poisson line patterns
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-21
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Covering random points in a unit disk
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 22-30
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
On weak stationarity and weak isotropy of processes of convex bodies and cylinders
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 864-882
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
On the correlation between the volumes of the typical Poisson-Voronoi cell and the typical Stienen sphere
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 883-892
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
On a Model for the Storage of Files on a Hardware. II. Evolution of a Typical Data Block
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 901-927
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Retrieving convex bodies from restricted covariogram functions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 613-629
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
The Hausdorff dimension of a class of random self-similar fractal trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 708-730
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Identities linking volumes of convex hulls
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 630-644
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Intersection densities of nonstationary Poisson processes of hypersurfaces
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 307-317
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Explicit laws of large numbers for random nearest-neighbour-type graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 326-342
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Some distributional results for Poisson-Voronoi tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 16-40
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
The surface pair correlation function for stationary Boolean models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-15
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
A connection between the volume fractions of the Stienen model and the dead leaves model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 41-52
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Multitype shape theorems for first passage percolation models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 53-76
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
On Second-Order Characteristics of Germ-Grain Models with Convex Grains
- Part of
-
- Journal:
- Mathematika / Volume 53 / Issue 2 / December 2006
- Published online by Cambridge University Press:
- 21 December 2009, pp. 255-285
- Print publication:
- December 2006
-
- Article
- Export citation
A Large Deviations Approach to the Geometry of Random Polytopes
- Part of
-
- Journal:
- Mathematika / Volume 53 / Issue 2 / December 2006
- Published online by Cambridge University Press:
- 21 December 2009, pp. 173-210
- Print publication:
- December 2006
-
- Article
- Export citation
Navigation in small-world networks: a scale-free continuum model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1173-1180
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
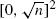 satisfying a weak equidistribution assumption. We show that if the first excess is
satisfying a weak equidistribution assumption. We show that if the first excess is 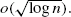
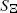 of a stationary Boolean model
of a stationary Boolean model  with grains from the convex ring is considered. A sufficient condition and a necessary condition for the existence of the density of the second-order moment measure of
with grains from the convex ring is considered. A sufficient condition and a necessary condition for the existence of the density of the second-order moment measure of 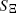 are given and a representation of this density is derived. As applications, the surface pair correlation functions of a Boolean model with spheres and a Boolean model with randomly oriented right circular cylinders in ℝ
are given and a representation of this density is derived. As applications, the surface pair correlation functions of a Boolean model with spheres and a Boolean model with randomly oriented right circular cylinders in ℝ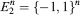 . Understanding the complexity of this class of polytopes is important for the “polyhedral combinatorics” approach to combinatorial optimization, and was put forward by Ziegler in [
. Understanding the complexity of this class of polytopes is important for the “polyhedral combinatorics” approach to combinatorial optimization, and was put forward by Ziegler in [