At each point of a Poisson point process of intensity λ in the hyperbolic plane, center a ball of bounded random radius. Consider the probability P r that, from a fixed point, there is some direction in which one can reach distance r without hitting any ball. It is known (see Benjamini, Jonasson, Schramm and Tykesson (2009)) that if λ is strictly smaller than a critical intensity λ gv thenP r does not go to 0 as r → ∞. The main result in this note shows that in the case λ=λ gv, the probability of reaching a distance larger than r decays essentially polynomially, while if λ>λ gv, the decay is exponential. We also extend these results to various related models and we finally obtain asymptotic results in several situations.

The almost-sure connectivity of the Euclidean minimal spanning forest MSF(X) on a homogeneous Poisson point process X ⊂ ℝd is an open problem for dimension d>2. We introduce a descending family of graphs (G n )n ≥2 that can be seen as approximations to the MSF in the sense that MSF(X)=∩n=2 ∞G n (X). For n=2, one recovers the relative neighborhood graph or, in other words, the β-skeleton with β=2. We show that almost-sure connectivity of G n (X) holds for all n≥2, all dimensions d≥2, and also point processes X more general than the homogeneous Poisson point process. In particular, we show that almost-sure connectivity holds if certain continuum percolation thresholds are strictly positive or, more generally, if almost surely X does not admit generalized descending chains.

We investigate the ray-length distributions for two different rectangular versions of Gilbert's tessellation (see Gilbert (1967)). In the full rectangular version, lines extend either horizontally (east- and west-growing rays) or vertically (north- and south-growing rays) from seed points which form a Poisson point process, each ray stopping when another ray is met. In the half rectangular version, east- and south-growing rays do not interact with west and north rays. For the half rectangular tessellation, we compute analytically, via recursion, a series expansion for the ray-length distribution, whilst, for the full rectangular version, we develop an accurate simulation technique, based in part on the stopping-set theory for Poisson processes (see Zuyev (1999)), to accomplish the same. We demonstrate the remarkable fact that plots of the two distributions appear to be identical when the intensity of seeds in the half model is twice that in the full model. In this paper we explore this coincidence, mindful of the fact that, for one model, our results are from a simulation (with inherent sampling error). We go on to develop further analytic theory for the half-Gilbert model using stopping-set ideas once again, with some novel features. Using our theory, we obtain exact expressions for the first and second moments of the ray length in the half-Gilbert model. For all practical purposes, these results can be applied to the full-Gilbert model—as much better approximations than those provided by Mackisack and Miles (1996).

For stationary fiber processes, the estimation of the directional distribution is an important task. We consider a stereological approach, assuming that the intersection points of the process with a finite number of test hyperplanes can be observed in a bounded window. The intensity of these intersection processes is proportional to the cosine transform of the directional distribution. We use the approximate inverse method to invert the cosine transform and analyze asymptotic properties of the estimator in growing windows for Poisson line processes. We show almost-sure convergence of the estimator and derive Berry–Esseen bounds, including formulae for the variance.

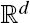For a Borel set A and a homogeneous Poisson point process η in of intensity λ>0, define the Poisson–Voronoi approximation A η of A as a union of all Voronoi cells with nuclei from η lying in A. If A has a finite volume and perimeter, we find an exact asymptotic of E Vol(AΔ A η) as λ→∞, where Vol is the Lebesgue measure. Estimates for all moments of Vol(A η) and Vol(AΔ A η) together with their asymptotics for large λ are obtained as well.

We introduce the entropy of a family of planar curves in terms of the number of intersections of the family with a random line, calculate it for key examples, and discuss the entropy of a pattern of rings produced by an impulse on the surface of still water.

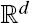We aim to link random fields and marked point processes, and, therefore, introduce a new class of stochastic processes which are defined on a random set in . Unlike for random fields, the mark covariance function of a random marked set is in general not positive definite. This implies that in many situations the use of simple geostatistical methods appears to be questionable. Surprisingly, for a special class of processes based on Gaussian random fields, we do have positive definiteness for the corresponding mark covariance function and mark correlation function.

In this paper we consider three-dimensional random tessellations that are stable under iteration (STIT tessellations). STIT tessellations arise as a result of subsequent cell division, which implies that their cells are not face-to-face. The edges of the cell-dividing polygons are the so-called I-segments of the tessellation. The main result is an explicit formula for the distribution of the number of vertices in the relative interior of the typical I-segment. In preparation for its proof, we obtain other distributional identities for the typical I-segment and the length-weighted typical I-segment, which provide new insight into the spatiotemporal construction process.

Given a rectangle containing uniformly distributed random points, how far are the points from the rectangle’s centre? In this paper we provide closed-form expressions for the cumulative distribution function and probability density function that characterise the distance. An expression for the average distance to the centre of the rectangle is also provided.

Motivated by set estimation problems, we consider three closely related shape conditions for compact sets: positive reach, r-convexity, and the rolling condition. First, the relations between these shape conditions are analyzed. Second, for the estimation of sets fulfilling a rolling condition, we obtain a result of ‘full consistency’ (i.e. consistency with respect to the Hausdorff metric for the target set and for its boundary). Third, the class of uniformly bounded compact sets whose reach is not smaller than a given constant r is shown to be a P-uniformity class (in Billingsley and Topsøe's (1967) sense) and, in particular, a Glivenko-Cantelli class. Fourth, under broad conditions, the r-convex hull of the sample is proved to be a fully consistent estimator of an r-convex support in the two-dimensional case. Moreover, its boundary length is shown to converge (almost surely) to that of the underlying support. Fifth, the above results are applied to obtain new consistency statements for level set estimators based on the excess mass methodology (see Polonik (1995)).

Given two independent Poisson point processes Φ(1), Φ(2) in , the AB Poisson Boolean model is the graph with the points of Φ(1) as vertices and with edges between any pair of points for which the intersection of balls of radius 2r centered at these points contains at least one point of Φ(2). This is a generalization of the AB percolation model on discrete lattices. We show the existence of percolation for all d ≥ 2 and derive bounds for a critical intensity. We also provide a characterization for this critical intensity when d = 2. To study the connectivity problem, we consider independent Poisson point processes of intensities n and τn in the unit cube. The AB random geometric graph is defined as above but with balls of radius r. We derive a weak law result for the largest nearest-neighbor distance and almost-sure asymptotic bounds for the connectivity threshold.

In this paper we introduce the transparent dead leaves (TDL) random field, a new germ-grain model in which the grains are combined according to a transparency principle. Informally, this model may be seen as the superposition of infinitely many semitransparent objects. It is therefore of interest in view of the modeling of natural images. Properties of this new model are established and a simulation algorithm is proposed. The main contribution of the paper is to establish a central limit theorem, showing that, when varying the transparency of the grain from opacity to total transparency, the TDL model ranges from the dead leaves model to a Gaussian random field.

The Blaschke–Petkantschin formula is a geometric measure decomposition of the q-fold product of Lebesgue measure on ℝn. Here we discuss another decomposition called polar decomposition by considering ℝn×⋯×ℝn as ℳn×k and using its polar decomposition. This is a generalisation of the Blaschke–Petkantschin formula and may be useful when one needs to integrate a function g:ℝn×⋯×ℝn→ℝ with rotational symmetry, that is, for each orthogonal transformation O,g(O(x1),…,O(xk))=g(x1,…xk). As an application we compute the moments of a Gaussian determinant.

We study stochastic properties of the empty space for stationary germ-grain models in R d ; in particular, we deal with the inner radius of the empty space with respect to a general structuring element which is allowed to be lower dimensional. We consider Poisson cluster and mixed Poisson germ-grain models, and show in several situations that more variability results in stochastically greater empty space in terms of the empty space hazard function. Furthermore, we study the asymptotic behaviour of the empty space hazard functions at 0 and at ∞.

A navigation on a set of points S is a rule for choosing which point to move to from the present point in order to progress toward a specified target. We study some navigations in the plane where S is a nonuniform Poisson point process (in a finite domain) with intensity going to +∞. We show the convergence of the traveller's path lengths, and give the number of stages and the geometry of the traveller's trajectories, uniformly for all starting points and targets, for several navigations of geometric nature. Other costs are also considered. This leads to asymptotic results on the stretch factors of random Yao graphs and random θ-graphs.

Tessellations of R 3 that use convex polyhedral cells to fill the space can be extremely complicated. This is especially so for tessellations which are not ‘facet-to-facet’, that is, for those where the facets of a cell do not necessarily coincide with the facets of that cell's neighbours. Adjacency concepts between neighbouring cells (or between neighbouring cell elements) are not easily formulated when facets do not coincide. In this paper we make the first systematic study of these topological relationships when a tessellation of R 3 is not facet-to-facet. The results derived can also be applied to the simpler facet-to-facet case. Our study deals with both random tessellations and deterministic ‘tilings’. Some new theory for planar tessellations is also given.

We consider statistical inference for a parametric cooperative sequential adsorption model for spatial time series data, based on maximum likelihood. We establish asymptotic normality of the maximum likelihood estimator in the thermodynamic limit. We also perform and discuss some numerical simulations of the model, which illustrate the procedure for creating confidence intervals for large samples.

Consider the region L = {(x, y): 0 ≤ y ≤ Clog(1 + x), x > 0} for a constant C > 0. We study the percolation and coverage properties of this region. For the coverage properties, we place a Poisson point process of intensity λ on the entire half space R + x R and associated with each Poisson point we place a box of a random side length ρ. Depending on the tail behaviour of the random variable ρ we exhibit a phase transition in the intensity for the eventual coverage of the region L. For the percolation properties, we place a Poisson point process of intensity λ on the region R 2. At each point of the process we centre a box of a random side length ρ. In the case ρ ≤ R for some fixed R > 0 we study the critical intensity λc of the percolation on L.

We consider a queue where the server is the Euclidean space, and the customers are random closed sets (RACSs) of the Euclidean space. These RACSs arrive according to a Poisson rain and each of them has a random service time (in the case of hail falling on the Euclidean plane, this is the height of the hailstone, whereas the RACS is its footprint). The Euclidean space serves customers at speed 1. The service discipline is a hard exclusion rule: no two intersecting RACSs can be served simultaneously and service is in the first-in–first-out order, i.e. only the hailstones in contact with the ground melt at speed 1, whereas the others are queued. A tagged RACS waits until all RACSs that arrived before it and intersecting it have fully melted before starting its own melting. We give the evolution equations for this queue. We prove that it is stable for a sufficiently small arrival intensity, provided that the typical diameter of the RACS and the typical service time have finite exponential moments. We also discuss the percolation properties of the stationary regime of the RACS in the queue.

Consider a random simplex in a d-dimensional convex body which is the convex hull of d+1 random points from the body. We study the following question: as a function of the convex body, is the expected volume of such a random simplex monotone non-decreasing under inclusion? We show that this is true when d is 1 or 2, but does not hold for d≥4. We also prove similar results for higher moments of the volume of a random simplex, in particular for the second moment, which corresponds to the determinant of the covariance matrix of the convex body. 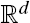These questions are motivated by the slicing conjecture.