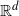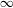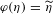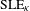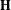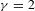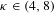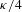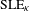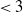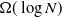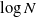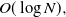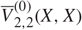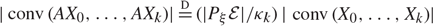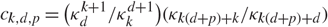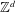Refine listing
Actions for selected content:
423 results in 60Dxx
Interaction of Poisson hyperplane processes and convex bodies
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 11 December 2019, pp. 1020-1032
- Print publication:
- December 2019
-
- Article
- Export citation
Simple Formulas for Constellations and Bipartite Maps with Prescribed Degrees
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 12 November 2019, pp. 160-176
- Print publication:
- February 2021
-
- Article
- Export citation
UNIFORM SPANNING FORESTS OF PLANAR GRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 13 September 2019, e29
-
- Article
-
- You have access
- Open access
- Export citation
UNIQUENESS OF THE WELDING PROBLEM FOR SLE AND LIOUVILLE QUANTUM GRAVITY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 05 July 2019, pp. 757-783
- Print publication:
- May 2021
-
- Article
- Export citation
The diameter of KPKVB random graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 358-377
- Print publication:
- June 2019
-
- Article
- Export citation
Determination of Boolean models by densities of mixed volumes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 22 July 2019, pp. 116-135
- Print publication:
- March 2019
-
- Article
- Export citation
Random affine simplexes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 39-51
- Print publication:
- March 2019
-
- Article
- Export citation
Geometry of Uniform Spanning Forest Components in High Dimensions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1297-1321
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
A Boltzmann Approach to Percolation on Random Triangulations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1-43
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
A conditional limit theorem for high-dimensional ℓᵖ-spheres
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1060-1077
- Print publication:
- December 2018
-
- Article
- Export citation
On the critical threshold for continuum AB percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1228-1237
- Print publication:
- December 2018
-
- Article
- Export citation
Variance estimates for random disc-polygons in smooth convex discs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1143-1157
- Print publication:
- December 2018
-
- Article
- Export citation
Nearest-neighbour Markov point processes on graphs with Euclidean edges
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1275-1293
- Print publication:
- December 2018
-
- Article
- Export citation
Regenerative processes for Poisson zero polytopes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1217-1226
- Print publication:
- December 2018
-
- Article
- Export citation
Dilation volumes of sets of finite perimeter
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1095-1118
- Print publication:
- December 2018
-
- Article
- Export citation
Gilbert's disc model with geostatistical marking
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1075-1094
- Print publication:
- December 2018
-
- Article
- Export citation
Limit theorems for random polytopes with vertices on convex surfaces
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1227-1245
- Print publication:
- December 2018
-
- Article
- Export citation
Reach of repulsion for determinantal point processes in high dimensions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 760-788
- Print publication:
- September 2018
-
- Article
- Export citation
Pair correlation functions and limiting distributions of iterated cluster point processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 789-809
- Print publication:
- September 2018
-
- Article
- Export citation
Identification and isotropy characterization of deformed random fields through excursion sets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 706-725
- Print publication:
- September 2018
-
- Article
- Export citation