Refine listing
Actions for selected content:
1829 results in 60Gxx
On maximum family size in branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 632-643
- Print publication:
- September 1999
-
- Article
- Export citation
On the linear prediction of some Lp random fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 1 / August 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 31-50
- Print publication:
- August 1999
-
- Article
-
- You have access
- Export citation
Stopping sets: Gamma-type results and hitting properties
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 355-366
- Print publication:
- June 1999
-
- Article
- Export citation
Abel-Gontcharoff pseudopolynomials and the exact final outcome of SIR epidemic models (III)
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 532-550
- Print publication:
- June 1999
-
- Article
- Export citation
Ornstein–Uhlenbeck type processes with non-normal distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 389-402
- Print publication:
- June 1999
-
- Article
- Export citation
On the time-dependent occupancy and backlog distributions for the GI/G/∞ queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 558-569
- Print publication:
- June 1999
-
- Article
- Export citation
Reaching goals by a deadline: digital options and continuous-time active portfolio management
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 551-577
- Print publication:
- June 1999
-
- Article
- Export citation
Central limit theorem for a class of random measures associated with germ-grain models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 283-314
- Print publication:
- June 1999
-
- Article
- Export citation
Tail probabilities for non-standard risk and queueing processes with subexponential jumps
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 422-447
- Print publication:
- June 1999
-
- Article
- Export citation
On connected component Markov point processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 279-282
- Print publication:
- June 1999
-
- Article
- Export citation
Quermass-interaction processes: conditions for stability
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 315-342
- Print publication:
- June 1999
-
- Article
- Export citation
The maximum of a function of a Markov chain and application to linkage analysis
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 510-531
- Print publication:
- June 1999
-
- Article
- Export citation
Prediction of shot noise
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 374-388
- Print publication:
- June 1999
-
- Article
- Export citation
Super-replication in stochastic volatility models under portfolio constraints
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 523-545
- Print publication:
- June 1999
-
- Article
- Export citation
Weak convergence to the coalescent in neutral population models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 446-460
- Print publication:
- June 1999
-
- Article
- Export citation
Loss networks and Markov random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 403-414
- Print publication:
- June 1999
-
- Article
- Export citation
Continuity for multi-type branching processes with varying environments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 139-145
- Print publication:
- March 1999
-
- Article
- Export citation
Extension of Wald's first lemma to Markov processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 48-59
- Print publication:
- March 1999
-
- Article
- Export citation
Large deviations, moderate deviations, and queues with long-range dependent input
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 254-278
- Print publication:
- March 1999
-
- Article
- Export citation
On the supremum distribution of integrated stationary Gaussian processes with negative linear drift
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 135-157
- Print publication:
- March 1999
-
- Article
- Export citation
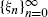 satisfies certain ergodicity properties, we then show that 𝔼
satisfies certain ergodicity properties, we then show that 𝔼