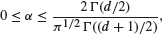Refine listing
Actions for selected content:
1828 results in 60Gxx
Surprising optimal estimators for the area fraction
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 995-1001
- Print publication:
- December 1999
-
- Article
- Export citation
Identifiability for non-stationary spatial structure
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1244-1250
- Print publication:
- December 1999
-
- Article
- Export citation
Stochastic comparisons for residual lifetimes and Bayesian notions of multivariate ageing
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1078-1094
- Print publication:
- December 1999
-
- Article
- Export citation
Asymptotic distribution of sum and maximum for Gaussian processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1031-1044
- Print publication:
- December 1999
-
- Article
- Export citation
Sequential selection of an increasing subsequence from a sample of random size
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1074-1085
- Print publication:
- December 1999
-
- Article
- Export citation
Incomplete markets: convergence of options values under the minimal martingale measure
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1058-1077
- Print publication:
- December 1999
-
- Article
- Export citation
Outcomes of epidemic models with general infection and removal rate functions at certain stopping times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 799-813
- Print publication:
- September 1999
-
- Article
- Export citation
On the size of a random sphere of influence graph
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 596-609
- Print publication:
- September 1999
-
- Article
- Export citation
On records and related processes for sequences with trends
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 668-681
- Print publication:
- September 1999
-
- Article
- Export citation
Favorable red and black on the integers with a minimum bet
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 837-851
- Print publication:
- September 1999
-
- Article
- Export citation
On the fractal dimensions of point patterns
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 643-663
- Print publication:
- September 1999
-
- Article
- Export citation
On the probabilistic properties of a double threshold ARMA conditional heteroskedastic model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 688-705
- Print publication:
- September 1999
-
- Article
- Export citation
The volume fraction of a Poisson germ model with maximally non-overlapping spherical grains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 610-624
- Print publication:
- September 1999
-
- Article
- Export citation
Isotropic correlation functions on d-dimensional balls
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 625-631
- Print publication:
- September 1999
-
- Article
- Export citation
Search schemes for random optimization algorithms that preserve the asymptotic distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 825-836
- Print publication:
- September 1999
-
- Article
- Export citation
Interacting particle systems approximations of the Kushner-Stratonovitch equation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 819-838
- Print publication:
- September 1999
-
- Article
- Export citation
The size of the connected components of excursion sets of χ2, t and F fields
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 579-595
- Print publication:
- September 1999
-
- Article
- Export citation
Interdependences of directional quantities of planar tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 664-678
- Print publication:
- September 1999
-
- Article
- Export citation
Large deviations for the time of ruin
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 733-746
- Print publication:
- September 1999
-
- Article
- Export citation
On maximum family size in branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 632-643
- Print publication:
- September 1999
-
- Article
- Export citation
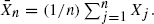 Under some mild regularity conditions on
Under some mild regularity conditions on 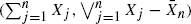 is obtained. Continuous-time results are also presented as well as a tube formula tail area approximation to the joint distribution of the sum and maximum.
is obtained. Continuous-time results are also presented as well as a tube formula tail area approximation to the joint distribution of the sum and maximum.