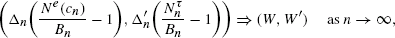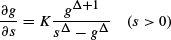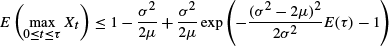Refine listing
Actions for selected content:
1827 results in 60Gxx
Extreme values of phase-type and mixed random variables with parallel-processing examples
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 194-210
- Print publication:
- March 1999
-
- Article
- Export citation
Estimating the reduced moments of a random measure
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 48-62
- Print publication:
- March 1999
-
- Article
- Export citation
Smallest-fit selection of random sizes under a sum constraint: weak convergence and moment comparisons
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 178-198
- Print publication:
- March 1999
-
- Article
- Export citation
Central limit theorem for wave-functionals of Gaussian processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 158-177
- Print publication:
- March 1999
-
- Article
- Export citation
Perfect simulation of some point processes for the impatient user
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 69-87
- Print publication:
- March 1999
-
- Article
- Export citation
Simple conditions for the convergence of simulated annealing type algorithms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 885-892
- Print publication:
- December 1998
-
- Article
- Export citation
Weak convergence on randomly deleted sets
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 893-902
- Print publication:
- December 1998
-
- Article
- Export citation
A uniform convergence theorem for the numerical solving of the nonlinear filtering problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 873-884
- Print publication:
- December 1998
-
- Article
- Export citation
On the optimality of repair-cost-limit policies
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 936-949
- Print publication:
- December 1998
-
- Article
- Export citation
Optimal stopping and maximal inequalities for geometric Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 856-872
- Print publication:
- December 1998
-
- Article
- Export citation
Stability index for products of random transformations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 968-988
- Print publication:
- December 1998
-
- Article
- Export citation
Rough descriptions of ruin for a general class of surplus processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1008-1026
- Print publication:
- December 1998
-
- Article
- Export citation
Some stationary processes in discrete and continuous time
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 989-1007
- Print publication:
- December 1998
-
- Article
- Export citation
One-dimensional loss networks and conditioned M/G/∞ queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 963-975
- Print publication:
- December 1998
-
- Article
- Export citation
Contact and chord length distribution of a stationary Voronoi tessellation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 603-618
- Print publication:
- September 1998
-
- Article
- Export citation
Optimal multivariate stopping rules
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 693-706
- Print publication:
- September 1998
-
- Article
- Export citation
A central limit theorem for conditionally centred random fields with an application to Markov fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 608-621
- Print publication:
- September 1998
-
- Article
- Export citation
A point process model with stochastic intensities for a branching population of two dependent types
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 723-739
- Print publication:
- September 1998
-
- Article
- Export citation
A boundary crossing probability for the Bessel process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 807-830
- Print publication:
- September 1998
-
- Article
- Export citation
The Maclaurin series for performance functions of Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 676-692
- Print publication:
- September 1998
-
- Article
- Export citation