Refine listing
Actions for selected content:
1827 results in 60Gxx
Stochastic fm models and non-linear time series analysis
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 986-1003
- Print publication:
- December 1997
-
- Article
- Export citation
On the rate of convergence for extremes of mean square differentiable stationary normal processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 908-923
- Print publication:
- December 1997
-
- Article
- Export citation
A secretary problem with two decision makers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1068-1074
- Print publication:
- December 1997
-
- Article
- Export citation
On some regularity conditions of Borel measures on R
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 218-224
- Print publication:
- October 1997
-
- Article
-
- You have access
- Export citation
Filtering of a branching process given its split times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 565-574
- Print publication:
- September 1997
-
- Article
- Export citation
A power-law model and other models for long-range dependence
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 657-670
- Print publication:
- September 1997
-
- Article
- Export citation
A stationary Poisson departure process from a minimally delayed infinite server queue with non-stationary Poisson arrivals
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 767-772
- Print publication:
- September 1997
-
- Article
- Export citation
Linear Programming Estimators and Bootstrapping for Heavy Tailed Phenomena
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 759-805
- Print publication:
- September 1997
-
- Article
- Export citation
Sengupta's invariant relationship and its application to waiting time inference
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 795-799
- Print publication:
- September 1997
-
- Article
- Export citation
Heavy traffic analysis for continuous polling models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 720-732
- Print publication:
- September 1997
-
- Article
- Export citation
Strong Approximations of Irreducible Closed Queueing Networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 498-522
- Print publication:
- June 1997
-
- Article
- Export citation
Orthogonal representations of random fields and an application to geophysics data
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 458-476
- Print publication:
- June 1997
-
- Article
- Export citation
A proof of the persistence criterion for a class of superprocesses
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 559-563
- Print publication:
- June 1997
-
- Article
- Export citation
Scanning Brownian Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 295-326
- Print publication:
- June 1997
-
- Article
- Export citation
Applications of Borovkov's Renovation Theory to Non-Stationary Stochastic Recursive Sequences and Their Control
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 388-413
- Print publication:
- June 1997
-
- Article
- Export citation
Duration of a secretary problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 556-558
- Print publication:
- June 1997
-
- Article
- Export citation
A unique representation theorem for the conditional expectation of stationary processes and application to dynamic estimation problems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 372-380
- Print publication:
- June 1997
-
- Article
- Export citation
Large deviations of heavy-tailed random sums with applications in insurance and finance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 293-308
- Print publication:
- June 1997
-
- Article
- Export citation
Unification of Software Reliability Models by Self-Exciting Point Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 337-352
- Print publication:
- June 1997
-
- Article
- Export citation
On wald-type optimal stopping for Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 66-73
- Print publication:
- March 1997
-
- Article
- Export citation
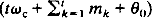 , where the message process {
, where the message process {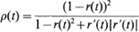
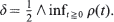 . We give bounds which are roughly of order
. We give bounds which are roughly of order 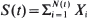 ,
, 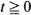 , where
, where 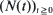 are non-negative integer-valued random variables and are
are non-negative integer-valued random variables and are 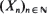 i.i.d. non-negative random variables with common distribution function
i.i.d. non-negative random variables with common distribution function 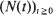 . Special attention is paid to the compound Poisson process and its ramifications. The right tail of the distribution function
. Special attention is paid to the compound Poisson process and its ramifications. The right tail of the distribution function 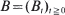 is standard Brownian motion and the supremum is taken over all stopping times
is standard Brownian motion and the supremum is taken over all stopping times 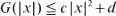 for some
for some 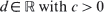 being given and fixed. The optimal stopping time is shown to be the hitting time by the reflecting Brownian motion
being given and fixed. The optimal stopping time is shown to be the hitting time by the reflecting Brownian motion 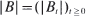 of the set of all (approximate) maximum points of the map
of the set of all (approximate) maximum points of the map 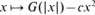 . The method of proof relies upon Wald's identity for Brownian motion and simple real analysis arguments. A simple proof of the Dubins–Jacka–Schwarz–Shepp–Shiryaev (square root of two) maximal inequality for randomly stopped Brownian motion is given as an application.
. The method of proof relies upon Wald's identity for Brownian motion and simple real analysis arguments. A simple proof of the Dubins–Jacka–Schwarz–Shepp–Shiryaev (square root of two) maximal inequality for randomly stopped Brownian motion is given as an application.