Refine listing
Actions for selected content:
1827 results in 60Gxx
The range of a simple random walk on ℤ
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1014-1033
- Print publication:
- December 1996
-
- Article
- Export citation
Some characterizations of partial exchangeability
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 3 / December 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-359
- Print publication:
- December 1996
-
- Article
-
- You have access
- Export citation
Anticipative portfolio optimization
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1095-1122
- Print publication:
- December 1996
-
- Article
- Export citation
Portfolio choice and the Bayesian Kelly criterion
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1145-1176
- Print publication:
- December 1996
-
- Article
- Export citation
Stability and structural properties of stochastic storage networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1169-1180
- Print publication:
- December 1996
-
- Article
- Export citation
On identifiability and order of continuous-time aggregated Markov chains, Markov-modulated Poisson processes, and phase-type distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 640-653
- Print publication:
- September 1996
-
- Article
- Export citation
Approximate versions of Melamed's theorem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 472-489
- Print publication:
- September 1996
-
- Article
- Export citation
Principles for modelling financial markets
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 601-613
- Print publication:
- September 1996
-
- Article
- Export citation
A local proof of the Swiss Army formula of Palm calculus
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 909-914
- Print publication:
- September 1996
-
- Article
- Export citation
Superprophet inequalities for independent random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 904-908
- Print publication:
- September 1996
-
- Article
- Export citation
Finite-time optimal control of a process leaving an interval
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 714-728
- Print publication:
- September 1996
-
- Article
- Export citation
First crossing of basic counting processes with lower non-linear boundaries: A unified approach through pseudopolynomials (I)
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 853-876
- Print publication:
- September 1996
-
- Article
- Export citation
The secretary problem: minimizing the expected rank with I.I.D. random variables
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 828-852
- Print publication:
- September 1996
-
- Article
- Export citation
Time series models with univariate margins in the convolution-closed infinitely divisible class
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 664-677
- Print publication:
- September 1996
-
- Article
- Export citation
On Kingman's characteristic functional approach to Rényi's characterization of Poisson processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 439-442
- Print publication:
- September 1996
-
- Article
- Export citation
A stopping time concerning sphere data and its applications
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 674-686
- Print publication:
- September 1996
-
- Article
- Export citation
On the prediction of fractional Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 400-410
- Print publication:
- September 1996
-
- Article
- Export citation
Economies of scale in queues with sources having power-law large deviation scalings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 840-857
- Print publication:
- September 1996
-
- Article
- Export citation
A note on the point processes of rare events
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 654-663
- Print publication:
- September 1996
-
- Article
- Export citation
Asymptotic expansions for functionals of dilation of point processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 573-591
- Print publication:
- September 1996
-
- Article
- Export citation
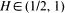 is discussed. The predictor
is discussed. The predictor 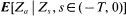 is represented as an integral with respect to
is represented as an integral with respect to 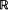 and
and 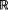
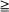 2, under transparent conditions, close to minimal. Formulas for higher-order derivatives allow one to construct asymptotical expansions. The results can be useful in sensitivity analysis, in light traffic theory for queues and for computation by simulation of derivatives at positive intensity, while the computation of the derivatives via statistical estimation of the functional itself and its increments usually gives poor results.
2, under transparent conditions, close to minimal. Formulas for higher-order derivatives allow one to construct asymptotical expansions. The results can be useful in sensitivity analysis, in light traffic theory for queues and for computation by simulation of derivatives at positive intensity, while the computation of the derivatives via statistical estimation of the functional itself and its increments usually gives poor results.