Refine listing
Actions for selected content:
1827 results in 60Gxx
Some diffusion models for the mabinogion sheep problem of williams
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 763-783
- Print publication:
- September 1996
-
- Article
- Export citation
Exact results for a secretary problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 630-639
- Print publication:
- September 1996
-
- Article
- Export citation
Integral equations for compound distribution functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 388-399
- Print publication:
- September 1996
-
- Article
- Export citation
A note on disjoint-occurrence inequalities for marked Poisson point processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 420-426
- Print publication:
- September 1996
-
- Article
- Export citation
On the full information best-choice problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 678-687
- Print publication:
- September 1996
-
- Article
- Export citation
Passage-time moments for continuous non-negative stochastic processes and applications
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 747-762
- Print publication:
- September 1996
-
- Article
- Export citation
Large deviations in the piecewise linear approximation of Gaussian processes with stationary increments
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 481-499
- Print publication:
- June 1996
-
- Article
- Export citation
Markov properties of cluster processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 346-355
- Print publication:
- June 1996
-
- Article
- Export citation
A point-process approach to almost-sure behaviour of record values and order statistics
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 426-462
- Print publication:
- June 1996
-
- Article
- Export citation
The Gaussian distribution revisited
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 500-524
- Print publication:
- June 1996
-
- Article
- Export citation
Random discrete distributions invariant under size-biased permutation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 525-539
- Print publication:
- June 1996
-
- Article
- Export citation
The sectional Poisson Voronoi tessellation is not a Voronoi tessellation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 356-376
- Print publication:
- June 1996
-
- Article
- Export citation
First passage time distribution of a Wiener process with drift concerning two elastic barriers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 164-175
- Print publication:
- March 1996
-
- Article
- Export citation
Dispersion of particle systems in Brownian flows
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 53-74
- Print publication:
- March 1996
-
- Article
- Export citation
On the asymptotic joint distribution of the sum and maximum of stationary normal random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 138-145
- Print publication:
- March 1996
-
- Article
- Export citation
Large deviations for discrete and continuous percolation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 29-52
- Print publication:
- March 1996
-
- Article
- Export citation
Poisson and compound Poisson approximations for random sums of random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 127-137
- Print publication:
- March 1996
-
- Article
- Export citation
An analysis of a modified M/G/1 queue using a martingale technique
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 224-238
- Print publication:
- March 1996
-
- Article
- Export citation
A flow conservation law for surface processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 13-28
- Print publication:
- March 1996
-
- Article
- Export citation
On evaluations and asymptotic approximations of first-passage-time probabilities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 270-284
- Print publication:
- March 1996
-
- Article
- Export citation
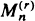 (the rth largest among a sample of
(the rth largest among a sample of 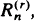 and differences and quotients involving them. In particular, we obtain characterizations of such asymptotic properties as
and differences and quotients involving them. In particular, we obtain characterizations of such asymptotic properties as 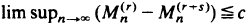 a.s. for some finite constant
a.s. for some finite constant 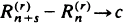 a.s. for some constant
a.s. for some constant 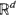 Of particular interest are the center of mass and the centered spatial second moments. Their asymptotic behavior depends strongly on the spatial dimension and the largest Lyapunov exponent of the flow. We use estimates for the pair separation process to give a fairly complete picture of this behavior as
Of particular interest are the center of mass and the centered spatial second moments. Their asymptotic behavior depends strongly on the spatial dimension and the largest Lyapunov exponent of the flow. We use estimates for the pair separation process to give a fairly complete picture of this behavior as 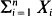 and
and 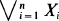 is derived under the condition
is derived under the condition 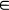 [0,∞). It is seen that the two statistics are asymptotically independent only if
[0,∞). It is seen that the two statistics are asymptotically independent only if 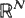 and
and 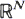 . The pair is jointly stationary, i.e. its distribution is invariant under translations. The vector field
. The pair is jointly stationary, i.e. its distribution is invariant under translations. The vector field 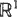 this specializes to a well-known rate conservation law for point processes. As an application, relationships for the linear contact distribution of Φ are derived.
this specializes to a well-known rate conservation law for point processes. As an application, relationships for the linear contact distribution of Φ are derived.