Refine listing
Actions for selected content:
1838 results in 60Gxx
The two-barrier problem for continuously differentiable processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 71-94
- Print publication:
- March 1992
-
- Article
- Export citation
Gaussian integrals on Wiener spaces
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 46-55
- Print publication:
- March 1992
-
- Article
- Export citation
Limit distributions of maximal segmental score among Markov-dependent partial sums
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 113-140
- Print publication:
- March 1992
-
- Article
- Export citation
Exact distribution theory for some point process record models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 20-44
- Print publication:
- March 1992
-
- Article
- Export citation
Nested variational inequalities and related optimal starting–stopping problems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 104-115
- Print publication:
- March 1992
-
- Article
- Export citation
A general risk process and its properties
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 73-81
- Print publication:
- March 1992
-
- Article
- Export citation
The maximum distribution of a Gaussian stochastic process indexed by a local field
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 1 / February 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 69-87
- Print publication:
- February 1989
-
- Article
-
- You have access
- Export citation
The growth of the expected number of real zeros of a random polynomial
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 1 / February 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 100-121
- Print publication:
- February 1989
-
- Article
-
- You have access
- Export citation
On non-uniform and global descriptions of the rate of convergence of Asymptotic expansions in the central limit theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 326-335
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Cumulants and partition lattices IV: a.s. convergence of generalised k-statistics
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 1 / August 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 79-94
- Print publication:
- August 1986
-
- Article
-
- You have access
- Export citation
Poisson convergence for point processes on the plane
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 253-269
- Print publication:
- October 1985
-
- Article
-
- You have access
- Export citation
On translation-bounded measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 1 / August 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 139-142
- Print publication:
- August 1984
-
- Article
-
- You have access
- Export citation
Random Fourier series on compact abelian hypergroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 1 / August 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 45-81
- Print publication:
- August 1984
-
- Article
-
- You have access
- Export citation
On domains of partial attraction
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 3 / June 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 328-331
- Print publication:
- June 1982
-
- Article
-
- You have access
- Export citation
Some Properties of stochastic compactness
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 3 / February 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 264-277
- Print publication:
- February 1981
-
- Article
-
- You have access
- Export citation
On the law of the iterated logarithm in the infinite variance case
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 1 / September 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 5-14
- Print publication:
- September 1980
-
- Article
-
- You have access
- Export citation
Relative stability, characteristic functions and stochastic compactness
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 499-509
- Print publication:
- December 1979
-
- Article
-
- You have access
- Export citation
On the rate of convergence of moments in the central limit theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 25 / Issue 2 / March 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 250-256
- Print publication:
- March 1978
-
- Article
-
- You have access
- Export citation
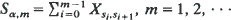 is determined by a realization
is determined by a realization 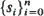 of states with s
of states with s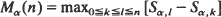 is derived. Computational methods with potential applications to the analysis of random Markov-dependent letter sequences (e.g. DNA and protein sequences) are presented.
is derived. Computational methods with potential applications to the analysis of random Markov-dependent letter sequences (e.g. DNA and protein sequences) are presented.