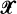Mecke's formula is concerned with a stationary random measure and shift-invariant measure on a locally compact Abelian group , and relates integrations concerning them to each other. For 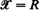, we generalize this to a pair of random measures which are jointly stationary. The resulting formula extends the so-called Swiss Army formula, which was recently obtained as a generalization for Little's formula. 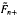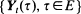The generalized Mecke formula, which is called GMF, can be also viewed as a generalization of the stationary version of H = λG. Under the stationary and ergodic assumptions, we apply it to derive many sample path formulas which have been known as extensions of H = λG. This will make clear what kinds of probabilistic conditions are sufficient to get them. We also mention a further generalization of Mecke's formula.

A generalized semi-Markov process with reallocation (RGSMP) was introduced to accommodate a large class of stochastic processes which cannot be analyzed by the well-known model of an ordinary generalized semi-Markov process (GSMP). For stationary RGSMP whose initial distribution has a product form, we show that, for a randomly chosen clock of a fixed insensitive type, if the lifetime of this clock is changed to infinity, then the background process is stationary under a certain time change. This implies that the expected time required for the tagged clock to consume a given amount x of resource, called the attained sojourn time, is a linear function of x. Such stationarity and linearity results are known for two special RGSMPs: ordinary GSMP and Kelly's symmetric queue. Our results not only extend them to a general RGSMP but also give more detailed formulas, which allow us to calculate for instance the expected attained sojourn time while the background process is in a given state. Furthermore, we remark that analogous results hold for GSMP with point-process input, in which the lifetimes of clocks of a fixed type form an arbitrary stationary sequence (of not necessarily independent random variables).

Monotonicity and correlation results for queueing network processes, generalized birth–death processes and generalized migration processes are obtained with respect to various orderings of the state space. We prove positive (e.g. association) and negative (e.g. negative association) correlations in space and positive correlations in time for different situations, in steady state as well as in the transient phase of the system. This yields exact bounds for joint probabilities in terms of their independent versions.

A recursive resampling method is discussed in this paper. Let X1, X2,…, Xn, be i.i.d. random variables with distribution function F and construct the empirical distribution function Fn. A new sample Xn+1 is drawn from Fn and the new empirical distribution function 1 in the wide sense, is computed from X1, X2,…, Xn, Xn+1. Then Xn+2 is drawn from 1 and 2 is obtained. In this way, Xn+m and m are found. It will be proved that m converges to a random variable almost surely as m goes to infinity and the limiting distribution is a compound beta distribution. In comparison with the usual non-recursive bootstrap, the main advantage of this procedure is a reduction in unconditional variance.

This paper provides an asymptotic estimate for the expected number of K-level crossings of the random trigonometric polynomial g1 cos x + g2 cos 2x+ … + gn cos nx where gj (j = 1, 2, …, n) are dependent normally distributed random variables with mean zero and variance one. The two cases of ρjr, the correlation coeffiecient between the j-th and r-th coefficients, being either (i) constant, or (ii) ρ∣j−r∣ρ, j ≠ r, 0 < ρ < 1, are considered. It is shown that the previous result for ρjr = 0 still remains valid for both cases.

In this paper, we develop the probabilistic foundations of the dynamic continuous choice problem. The underlying choice set is a compact metric space E such as the unit interval or the unit square. At each time point t, utilities for alternatives are given by a random function . To achieve a model of dynamic continuous choice, the theory of classical vector-valued extremal processes is extended to super-extremal processesY= {Yt, t > 0}. At any t > 0, Y t is a random upper semicontinuous function on a locally compact, separable, metric space E. General path properties of Y are discussed and it is shown that Y is Markov with state-space US(E). For each t > 0, Y t is associated.

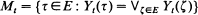For a compact metric E, we consider the argmax process M = {Mt, t > 0}, where . In the dynamic continuous choice application, the argmax process M represents the evolution of the set of random utility maximizing alternatives. M is a closed set-valued random process, and its path properties are investigated.

We consider the two-dimensional process {X(t), V(t)} where {V(t)} is Brownian motion with drift, and {X(t)} is its integral. In this note we derive the joint density function of T and V(T) where T is the time at which the process {X(t)} first returns to its initial value. A series expansion of the marginal density of T is given in the zero-drift case. When V(0) and the drift are both positive there is a positive probability that {Χ (t)} never returns to its initial value. We show how this probability grows for small drift. Finally, using the Kontorovich–Lebedev transform pair we obtain the escape probability explicitly for arbitrary values of the drift parameter.

The paper proposes a general model for pricing of derivative securities. The underlying dynamics follows stochastic equations involving anticipative stochastic integrals. These equations are solved explicitly and structural properties of solutions are studied.

Consider the convex hull of n independent, identically distributed points in the plane. Functionals of interest are the number of vertices Nn , the perimeter Ln and the area An of the convex hull. We study the asymptotic behaviour of these three quantities when the points are standard normally distributed. In particular, we derive the variances of Nn, Ln and An for large n and prove a central limit theorem for each of these random variables. We enlarge on a method developed by Groeneboom (1988) for uniformly distributed points supported on a bounded planar region. The process of vertices of the convex hull is of central importance. Poisson approximation and martingale techniques are used.

Three different stereological methods for the determination of second-order quantities of planar fibre processes which have been suggested in the literature are considered. Proofs of the formulae are given (also by using a new integral geometric formula), relations between the methods are derived and the prerequisites are discussed. Furthermore, edge-corrected unbiased estimators for the second-order quantities are given.

This paper shows how to calculate solutions to Poisson's equation for the waiting time sequence of the recurrent M/G/l queue. The solutions are used to construct martingales that permit us to study additive functionals associated with the waiting time sequence. These martingales provide asymptotic expressions, for the mean of additive functionals, that reflect dependence on the initial state of the process. In addition, we show how to explicitly calculate the scaling constants that appear in the central limit theorems for additive functionals of the waiting time sequence.

In this research, we present a statistical theory, and an algorithm, to identify one-pixel-wide closed object boundaries in gray-scale images. Closed-boundary identification is an important problem because boundaries of objects are major features in images. In spite of this, most statistical approaches to image restoration and texture identification place inappropriate stationary model assumptions on the image domain. One way to characterize the structural components present in images is to identify one-pixel-wide closed boundaries that delineate objects. By defining a prior probability model on the space of one-pixel-wide closed boundary configurations and appropriately specifying transition probability functions on this space, a Markov chain Monte Carlo algorithm is constructed that theoretically converges to a statistically optimal closed boundary estimate. Moreover, this approach ensures that any approximation to the statistically optimal boundary estimate will have the necessary property of closure.

In this paper we review conditions under which Wald's equation holds, mainly if the expectation of the given stopping time is infinite. As a main result we obtain what is probably the weakest possible version of Wald's equation for the case of independent, identically distributed (i.i.d.) random variables. Moreover, we improve a result of Samuel (1967) concerning the existence of stopping times for which the expectation of the stopped sum of the underlying i.i.d. 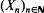sequence of random variables does not exist. Finally, we show by counterexamples that it is impossible to generalize a theorem of Kiefer and Wolfowitz (1956) relating the moments of the supremum of a random walk 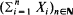with negative drift to moments of the positive part of X 1 to the case where the expectation of X 1 is —∞. Here, the Laplace–Stieltjes transform of the supremum of the considered random walk plays an important role.

We study a bivariate stochastic process {X(t)} = Z(t))}, where {XE (t)} is a continuous-time Markov chain describing the environment and {Z(t)} is the process of interest. In the context which motivated this study, {Z(t)} models the gating behaviour of a single ion channel. It is assumed that given {XE (t)}, the channel process {Z(t)} is a continuous-time Markov chain with infinitesimal generator at time t dependent on XE (t), and that the environment process {XE {t)} is not dependent on {Z(t)}. We derive necessary and sufficient conditions for {X(t)} to be time reversible, showing that then its equilibrium distribution has a product form which reflects independence of the state of the environment and the state of the channel. In the special case when the environment controls the speed of the channel process, we derive transition probabilities and sojourn time distributions for {Z(t)} by exploiting connections with Markov reward processes. Some of these results are extended to a stationary environment. Applications to problems arising in modelling multiple ion channel systems are discussed. In particular, we present ways in which a multichannel model in a random environment does and does not exhibit behaviour identical to a corresponding model based on independent and identically distributed channels.

The horizon ξ T (x) of a random field ζ (x, y) of right circular cones on a plane is investigated. It is supposed that bases of cones are centered at points sn = (xn , yn ), n = 1, 2, ···, on the (X, Y)-plane, constituting a Poisson point process S with intensity λ0 > 0 in a strip ΠT = {(x, y): – ∞< x <∞, 0 ≦ y ≦ T}, while altitudes of the cones h 1, h 2, · ·· are of the form hn = hn * + f(yn ), n = 1, 2, ···, where f(y) is an increasing continuous function on [0,∞), f(0) = 0, and h 1*, h 2*, · ·· is a sequence of i.i.d. positive random variables which are independent of the Poisson process S and have a distribution function F(h) with density p(h).

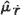Let denote the expected mean number of local maxima of the process 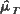ξ T (x) per unit length of the X-axis. We obtain an exact formula for under an arbitrary trend function 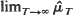f(y). Conditions sufficient for the limit being infinite are obtained in two cases: (a) h 1* has the uniform distribution in [0, H], f(y) = ky γ; (b) h 1* has the Rayleigh distribution, f(y) = k[log(y + 1)]γ . (In both cases γ 0 and 0 < k∞.) The corresponding sufficient conditions are: 0 < γ< 1 in case (a), 0 < γ< 1/2 in case (b).

Our aim in this article is to derive an expression for the best linear predictor of a multivariate symmetric α stable process based on many past values. For this purpose we introduce a definition of dispersion for symmetric α stable random vectors and choose the linear predictor which minimizes the dispersion of the error vector.

This paper considers a variation of the classical secretary problem; this variation allows for the interviewer to make an offer to previously interviewed applicants and for the applicant to reject an offer. In this version, the process ends after any offer is made. Two special cases are considered, where the optimal procedure and its probability of success are given for each. Furthermore, the problem is discussed in general and conditions for optimal strategies are given.

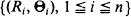A proposal is given for estimating the home range of an animal based on sequential sightings. We assume the given sightings are independent, identically distributed random vectors X 1,· ··, Xn whose common distribution has compact support. If are the polar coordinates of the sightings, then is a sup-measure and corresponds to the right endpoint of the distribution 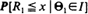. The corresponding upper semi-continuous function l(θ) is the boundary of the home range. We give a consistent estimator for the boundary l and under the assumption that the distribution of R 1 given is in the domain of attraction of an extreme value distribution with bounded support, we are able to give an approximate confidence region.

The stationary distribution for the population frequencies under an infinite alleles model is described as a random sequence (x 1, x 2, · ··) such that Σxi = 1. Likelihood ratio theory is developed for random samples drawn from such populations. As a result of the theory, it is shown that any parameter distinguishing an infinite alleles model with selection from the neutral infinite alleles model cannot be consistently estimated based on gene frequencies at a single locus. Furthermore, the likelihood ratio (neutral versus selection) converges to a non-trivial random variable under both hypotheses. This shows that if one wishes to test a completely specified infinite alleles model with selection against neutrality, the test will not obtain power 1 in the limit.

We prove a functional law of large numbers and a functional central limit theorem for a controlled renewal process, that is, a point process which differs from an ordinary renewal process in that the ith interarrival time is scaled by a function of the number of previous i arrivals. The functional law of large numbers expresses the convergence of a sequence of suitably scaled controlled renewal processes to the solution of an ordinary differential equation. Likewise, the functional central limit theorem establishes that the error in the law of large numbers converges weakly to the solution of a stochastic differential equation. Our proofs are based on martingale and time-change arguments.