Refine listing
Actions for selected content:
1838 results in 60Gxx
Boundary-crossing probabilities of some random fields related to likelihood ratio tests for epidemic alternatives
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 52-65
- Print publication:
- March 1993
-
- Article
- Export citation
Extreme values of the cyclostationary Gaussian random process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 82-97
- Print publication:
- March 1993
-
- Article
- Export citation
An extension of the Cameron–Martin result
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 247-251
- Print publication:
- March 1993
-
- Article
- Export citation
Slepian models for non-stationary Gaussian processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 98-111
- Print publication:
- March 1993
-
- Article
- Export citation
Joint exceedances of high levels under a local dependence condition
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 112-120
- Print publication:
- March 1993
-
- Article
- Export citation
Some characterizations of the Poisson process and geometric renewal process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 121-130
- Print publication:
- March 1993
-
- Article
- Export citation
Virtual customers in sensitivity and light traffic analysis via Campbell's formula for point processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 221-234
- Print publication:
- March 1993
-
- Article
- Export citation
Alternating projections and interpolation of stationary processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 921-931
- Print publication:
- December 1992
-
- Article
- Export citation
Random Johnson-Mehl tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 814-844
- Print publication:
- December 1992
-
- Article
- Export citation
Convex hulls of selected subsets of a Poisson process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 814-824
- Print publication:
- December 1992
-
- Article
- Export citation
Asymptotic analysis of extremes from autoregressive negative binomial processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 904-920
- Print publication:
- December 1992
-
- Article
- Export citation
Poisson approximation of intermediate empirical processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 825-837
- Print publication:
- December 1992
-
- Article
- Export citation
Extremal properties of the FIFO discipline in queueing networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 967-978
- Print publication:
- December 1992
-
- Article
- Export citation
The expected value of the one-sided cusum stopping time
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1008-1009
- Print publication:
- December 1992
-
- Article
-
- You have access
- Export citation
Generalised harmonic analysis of a class of nonstationary random fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 3 / December 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-401
- Print publication:
- December 1992
-
- Article
-
- You have access
- Export citation
New models for Markov random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 877-884
- Print publication:
- December 1992
-
- Article
- Export citation
An insensitivity property of ladder height distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 616-624
- Print publication:
- September 1992
-
- Article
- Export citation
Analyticity of Poisson-driven stochastic systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 532-541
- Print publication:
- September 1992
-
- Article
- Export citation
On equivalence of Markov properties over undirected graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 745-749
- Print publication:
- September 1992
-
- Article
- Export citation
Exploiting Markov chains to infer queue length from transactional data
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 713-732
- Print publication:
- September 1992
-
- Article
- Export citation
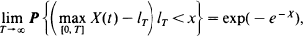
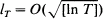 and all
and all 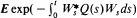 where
where 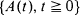 , with
, with 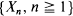 the sequence of interarrival times. We prove that, given a function
the sequence of interarrival times. We prove that, given a function 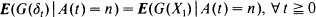 holds for a single positive integer
holds for a single positive integer 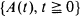 is a Poisson process. On the other hand, for a delayed renewal process
is a Poisson process. On the other hand, for a delayed renewal process 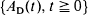 with
with 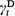 the residual life at
the residual life at 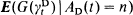 is independent of
is independent of 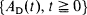 is an arbitrarily delayed Poisson process. We also give some corresponding results about characterizing the common distribution function
is an arbitrarily delayed Poisson process. We also give some corresponding results about characterizing the common distribution function  , where
, where 