Refine listing
Actions for selected content:
1838 results in 60Gxx
On the asymptotic distribution of the maximum number of infectives in epidemic models by immigration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 606-613
- Print publication:
- September 1994
-
- Article
- Export citation
A sample-path approach to Palm probabilities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 430-437
- Print publication:
- June 1994
-
- Article
- Export citation
The Beňes equations for the distribution of excursions for general storage processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 418-429
- Print publication:
- June 1994
-
- Article
- Export citation
On a distributional bound arising in autoregressive model fitting
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 401-408
- Print publication:
- June 1994
-
- Article
- Export citation
Rough limit results for level-crossing probabilities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 373-382
- Print publication:
- June 1994
-
- Article
- Export citation
Asymptotic properties of estimators for parameters of the Boolean model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 301-323
- Print publication:
- June 1994
-
- Article
- Export citation
Stochastic models of environmental pollution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 377-403
- Print publication:
- June 1994
-
- Article
- Export citation
Asymptotic Properties of Estimators for the Parameters of Spatial Inhomogeneous Poisson Point Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 122-154
- Print publication:
- March 1994
-
- Article
- Export citation
The Service Time Properties of an Unreliable Server Characterize the Exponential Distribution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 172-182
- Print publication:
- March 1994
-
- Article
- Export citation
Crossings of max-stable processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 130-138
- Print publication:
- March 1994
-
- Article
- Export citation
Local Maxima and the Expected Euler Characteristic of Excursion Sets of χ 2, F and t Fields
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 13-42
- Print publication:
- March 1994
-
- Article
- Export citation
Multivariate self-similar processes: second-order theory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 139-147
- Print publication:
- March 1994
-
- Article
- Export citation
Time-dependent rate conservation laws for a process defined with a stationary marked point process and their applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 114-129
- Print publication:
- March 1994
-
- Article
- Export citation
A strong law and a central limit theorem for controlled Galton-Watson processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 22-37
- Print publication:
- March 1994
-
- Article
- Export citation
On a best-choice problem by dependent criteria
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 221-234
- Print publication:
- March 1994
-
- Article
- Export citation
On the moments of ladder epochs for driftless random walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 201-205
- Print publication:
- 1994
-
- Article
- Export citation
Some characterizations of the exponential and geometric distributions arising in a queueing system with an unreliable server
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 985-990
- Print publication:
- December 1993
-
- Article
- Export citation
Modeling of repairable systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 926-938
- Print publication:
- December 1993
-
- Article
- Export citation
Absorption and first-passage times for a compound Poisson process in a general upper boundary
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 835-850
- Print publication:
- December 1993
-
- Article
- Export citation
Some results involving the maximum of Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 805-818
- Print publication:
- December 1993
-
- Article
- Export citation
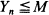 for
for 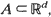 , with intensity function
, with intensity function 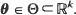 . In this article, we show that the maximum likelihood estimator
. In this article, we show that the maximum likelihood estimator 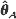 and the Bayes estimator
and the Bayes estimator 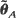 are consistent, asymptotically normal, and asymptotically efficient as the sample region
are consistent, asymptotically normal, and asymptotically efficient as the sample region  . These results extend asymptotic results of Kutoyants (1984), proved for an inhomogeneous Poisson process on [0,
. These results extend asymptotic results of Kutoyants (1984), proved for an inhomogeneous Poisson process on [0, 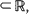 , where
, where 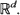 . Furthermore, a Cramér–Rao lower bound is found for any estimator
. Furthermore, a Cramér–Rao lower bound is found for any estimator 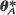 of
of 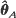 and
and 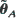 are considered for modulated (Cox (1972)), and linear Poisson processes.
are considered for modulated (Cox (1972)), and linear Poisson processes.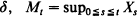 and
and 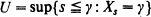 and Δ=
and Δ= 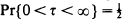 . We also derive various other distributional results involving the pair (
. We also derive various other distributional results involving the pair (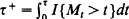 ; in particular we show that, in case
; in particular we show that, in case 