Exceedances of a non-stationary sequence above a boundary define certain point processes, which converge in distribution under mild mixing conditions to Poisson processes. We investigate necessary and sufficient conditions for the convergence of the point process of exceedances, the point process of upcrossings and the point process of clusters of exceedances. Smooth regularity conditions, as smooth oscillation of the non-stationary sequence, imply that these point processes converge to the same Poisson process. Since exceedances are asymptotically rare, the results are extended to triangular arrays of rare events.

In this paper, optimal stopping problems for semi-Markov processes are studied in a fairly general setting. In such a process transitions are made from state to state in accordance with a Markov chain, but the amount of time spent in each state is random. The times spent in each state follow a general renewal process. They may depend on the present state as well as on the state into which the next transition is made.

Our goal is to maximize the expected net return, which is given as a function of the state at time t minus some cost function. Discounting may or may not be considered. The main theorems (Theorems 3.5 and 3.11) are expressions for the optimal stopping time in the undiscounted and discounted case. These theorems generalize results of Zuckerman [16] and Boshuizen and Gouweleeuw [3]. Applications are given in various special cases.

The results developed in this paper can also be applied to semi-Markov shock models, as considered in Taylor [13], Feldman [6] and Zuckerman [15].

We propose a two-parameter family of conjugate prior distributions for the number of undiscovered objects in a class of Bayesian search models. The family contains the one-parameter Euler and Heine families as special cases. The two parameters may be interpreted respectively as an overall success rate and a rate of depletion of the source of objects. The new family gives enhanced flexibility in modelling.

A reference probability is explicitly constructed under which the signal and observation processes are independent. A simple, explicit recursive form is then obtained for the conditional density of the signal given the observations. Both non-linear and linear filters are considered, as well as two different information patterns.

For two-dimensional spatial data, a spatial unilateral autoregressive moving average (ARMA) model of first order is defined and its properties studied. The spatial correlation properties for these models are explicitly obtained, as well as simple conditions for stationarity and conditional expectation (interpolation) properties of the model. The multiplicative or linear-by-linear first-order spatial models are seen to be a special case which have proved to be of practical use in modeling of two-dimensional spatial lattice data, and hence the more general models should prove to be useful in applications. These unilateral models possess a convenient computational form for the exact likelihood function, which gives proper treatment to the border cell values in the lattice that have a substantial effect in estimation of parameters. Some simulation results to examine properties of the maximum likelihood estimator and a numerical example to illustrate the methods are briefly presented.

The full-information secretary problem in which the objective is to minimize the expected rank is seen to have a value smaller than 7/3 for all n (the number of options). This can be achieved by a simple memoryless threshold rule. The asymptotically optimal value for the class of such rules is about 2.3266. For a large finite number of options, the optimal stopping rule depends on the whole sequence of observations and seems to be intractable. This raises the question whether the influence of the history of all observations may asymptotically fade. We have not solved this problem, but we show that the values for finite n are non-decreasing in n and exhibit a sequence of lower bounds that converges to the asymptotic value which is not smaller than 1.908.

The two-point Markov chain boundary-value problem discussed in this paper is a finite-time version of the quasi-stationary behaviour of Markov chains. Specifically, for a Markov chain {Xt :t = 0, 1, ·· ·}, given the time interval (0, n), the interest is in describing the chain at some intermediate time point r conditional on knowing both the behaviour of the chain at the initial time point 0 and that over the interval (0, n) it has avoided some subset B of the state space. The paper considers both ‘real time' estimates for r = n (i.e. the chain has avoided B since 0), and a posteriori estimates for r < n with at least partial knowledge of the behaviour of Xn. Algorithms to evaluate the distribution of Xr can be as small as O(n 3) (and, for practical purposes, even O(n 2 log n)). The estimates may be stochastically ordered, and the process (and hence, the estimates) may be spatially homogeneous in a certain sense. Maximum likelihood estimates of the sample path are furnished, but by example we note that these ML paths may differ markedly from the path consisting of the expected or average states. The scope for two-point boundary-value problems to have solutions in a Markovian setting is noted.

Several examples are given, together with a discussion and examples of the analogous problem in continuous time. These examples include the basic M/G/k queue and variants that include a finite waiting room, reneging, balking, and Bernoulli feedback, a pure birth process and the Yule process. The queueing examples include Larson's (1990) ‘queue inference engine'.

We propose an AR(1) model that can be used to generate logistic processes. The proposed model has simple probability and correlation structure that can accommodate the full range of attainable correlation. The correlation structure and the joint distribution of the proposed model are given, as well as their conditional mean and variance.

The first-order autoregressive semi-Mittag-Leffler (SMLAR(1)) process is introduced and its properties are studied. As an illustration, we discuss the special case of the first-order autoregressive Mittag-Leffler (MLAR(1)) process.

We define a class of two-dimensional Markov random graphs with I, V, T and Y-shaped nodes (vertices). These are termed polygonal models. The construction extends our earlier work [1]– [5]. Most of the paper is concerned with consistent polygonal models which are both stationary and isotropic and which admit an alternative description in terms of the trajectories in space and time of a one-dimensional particle system with motion, birth, death and branching. Examples of computer simulations based on this description are given.

There are a number of cases in the theories of queues and dams where the limiting distribution of the pertinent processes is geometric with a modified initial term — herein called zero-modified geometric (ZMG). The paper gives a unified treatment of the various cases considered hitherto and some others by using a duality relation between random walks with impenetrable and with absorbing barriers, and deriving the probabilities of absorption by using Waldian identities. Thus the method enables us to distinguish between those cases where the limiting distribution would be ZMG and those where it would not.

A problem of optimal stopping of the discrete-time Markov process by two decision-makers (Player 1 and Player 2) in a competitive situation is considered. The zero-sum game structure is adopted. The gain function depends on states chosen by both decision-makers. When both players want to accept the realization of the Markov process at the same moment, the priority is given to Player 1. The construction of the value function and the optimal strategies for the players are given. The Markov chain case is considered in detail. An example related to the generalized secretary problem is solved.

Using a simple characterization of the Linnik distribution, discrete-time processes having a stationary Linnik distribution are constructed. The processes are structurally related to exponential processes introduced by Arnold (1989), Lawrance and Lewis (1981) and Gaver and Lewis (1980). Multivariate versions of the processes are also described. These Linnik models appear to be viable alternatives to stable processes as models for temporal changes in stock prices.

In a counting process considered at time t the focus is often on the length of the current interarrival time, whereas points in the past may be said to constitute information about the process. The paper introduces new concepts on how to quantify predictability of the future behavior of counting processes based on the past information and considers then situations in which the future points become more (or less) predictable. Various properties of our proposed concepts are studied and applications relevant to the reliability of repairable systems are given.

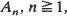Let , be i.i.d. random closed sets in 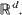. Limit theorems for their normalized convex hulls 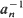conv (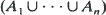) are proved. The limiting distributions correspond to 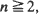C-stable random sets. The random closed set A is called C-stable if, for any , the sets 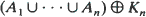anA and conv ( coincide in distribution for certain positive an, compact Kn , and independent copies A 1, …, An of A. The distributions of C-stable sets are characterized via corresponding containment functionals.

A simple model for the intensity of infection during an epidemic in a closed population is studied. It is shown that the size of an epidemic (i.e. the number of persons infected) and the cumulative force of an epidemic (i.e. the amount of infectiousness that has to be avoided by a person that will stay uninfected during the entire epidemic) satisfy an equation of balance. Under general conditions, small deviances from this balance are, in large populations, asymptotically mixed normally distributed. For some special epidemic models the size of an asymptotically large epidemic is asymptotically normally distributed.

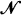A Markovian arrival stream is a marked point process generated by the state transitions of a given Markovian environmental process and Poisson arrival rates depending on the environment. It is shown that to a given marked point process there is a sequence of such Markovian arrival streams with the property that 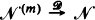as m →∞. Various related corollaries (involving stationarity, convergence of moments and ergodicity) and counterexamples are discussed as well.

The paper investigates stochastic processes directed by a randomized time process. A new family of directing processes called Hougaard processes is introduced. Monotonicity properties preserved under subordination, and dependence among processes directed by a common randomized time are studied. Results for processes subordinated to Poisson and stable processes are presented. Potential applications to shock models and threshold models are also discussed. Only Markov processes are considered.

We obtain a single formula which, when its components are adequately chosen, transforms itself into the main formulas of the Palm theory of point processes: Little's L = λW formula [10], Brumelle's H = λG formula [5], Neveu's exchange formula [14], Palm inversion formula and Miyazawa's rate conservation law [12]. It also contains various extensions of the above formulas and some new ones.

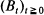Let be the Brownian motion process starting at the origin, 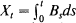its primitive and 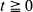Ut = (Xt+x + ty, Bt + y), , the associated bidimensional process starting from a point 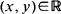. In this paper we present an elementary procedure for re-deriving the formula of Lefebvre (1989) giving the Laplace–Fourier transform of the distribution of the couple (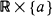σ α, Uσa ), as well as Lachal's (1991) formulae giving the explicit Laplace–Fourier transform of the law of the couple (σ ab, Uσab ), where σ α and σ ab denote respectively the first hitting time of from the right and the first hitting time of the double-sided barrier 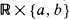by the process 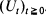. This method, which unifies and considerably simplifies the proofs of these results, is in fact a ‘vectorial' extension of the classical technique of Darling and Siegert (1953). It rests on an essential observation (Lachal (1992)) of the Markovian character of the bidimensional process .

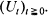Using the same procedure, we subsequently determine the Laplace–Fourier transform of the conjoint law of the quadruplet (σ α, Uσa, σb, Uσb ).