We consider two models for the control of a satellite–in the first, fuel is expended in a linear fashion to move a satellite following a diffusion–where the aim is to keep the satellite above a critical level for as long as possible (or indeed to reach a higher, ‘safe’ level). Under suitable assumptions for the drift and diffusion coefficients, it is shown that the stochastic maximum of the time to fall below the critical level is attained by a policy which imposes a reflecting boundary at the critical level until the fuel is exhausted and jumps the satellite directly to the safe level if this is ever possible. In the second model, there is a nonlinear response to the expenditure of fuel, and no safe level. It is shown that the optimal policy for maximizing the expected discounted time for the satellite to crash is similar, in that equal packets of fuel are used to jump the satellite upwards each time it reaches the critical level.

We study the present value Z ∞ = ∫0 ∞ e-X t- dY t where (X,Y) is an integrable Lévy process. This random variable appears in various applications, and several examples are known where the distribution of Z ∞ is calculated explicitly. Here sufficient conditions for Z ∞ to exist are given, and the possibility of finding the distribution of Z ∞ by Markov chain Monte Carlo simulation is investigated in detail. Then the same ideas are applied to the present value Z - ∞ = ∫0 ∞ exp{-∫0 t R s ds}dY t where Y is an integrable Lévy process and R is an ergodic strong Markov process. Numerical examples are given in both cases to show the efficiency of the Monte Carlo methods.

We consider a discrete-time financial market model with L 1 risky asset price process subject to proportional transaction costs. In this general setting, using a dual martingale representation we provide sufficient conditions for the super-replication cost to coincide with the replication cost. Next, we study the convergence problem in a stationary binomial model as the time step tends to zero, keeping the proportional transaction costs fixed. We derive lower and upper bounds for the limit of the super-replication cost. In the case of European call options and for a unit initial holding in the risky asset, the upper and lower bounds are equal. This result also holds for the replication cost of European call options. This is evidence (but not a proof) against the common opinion that the replication cost is infinite in a continuous-time model.

Very little is known about the quantitative behaviour of dynamical systems with random excitation, unless the system is linear. Known techniques imply the resolution of parabolic partial differential equations (Fokker–Planck–Kolmogorov equation), which are degenerate and of high dimension and for which there is no effective known method of resolution. Therefore, users (physicists, mechanical engineers) concerned with such systems have had to design global linearization techniques, known as equivalent statistical linearization (Roberts and Spanos (1990)). So far, there has been no rigorous justification of these techniques, with the notable exception of the paper by Kozin (1987). In this contribution, using large deviation principles, several mathematically founded linearization methods are proposed. These principles use relative entropy, or Kullback information, of two probability measures, and Donsker–Varadhan entropy of a Gaussian measure relatively to a Markov kernel. The method of ‘true linearization’ (Roberts and Spanos (1990)) is justified.

We consider the inverse problem of estimating the input random field in a stochastic integral equation relating two random fields. The purpose of this paper is to present an approach to this problem using a Riesz-based or orthonormal-based series expansion of the input random field with uncorrelated random coefficients. We establish conditions under which the input series expansion induces (via the integral equation) a Riesz-based or orthonormal-based series expansion for the output random field. The estimation problem is studied considering two cases, depending on whether data are available from either the output random field alone, or from both the input and output random fields. Finally, we discuss this approach in the case of transmissivity estimation from piezometric head data, which was the original motivation of this work.

A stochastic dynamical context is developed for Bookstein's shape theory. It is shown how Bookstein's shape space for planar triangles arises naturally when the landmarks are moved around by a special Brownian motion on the general linear group of invertible (2×2) real matrices. Asymptotics for the Brownian transition density are used to suggest an exponential family of distributions, which is analogous to the von Mises-Fisher spherical distribution and which has already been studied by J. K. Jensen. The computer algebra implementation Itovsn3 (W. S. Kendall) of stochastic calculus is used to perform the calculations (some of which actually date back to work by Dyson on eigenvalues of random matrices and by Dynkin on Brownian motion on ellipsoids). An interesting feature of these calculations is that they include the first application (to the author's knowledge) of the Gröbner basis algorithm in a stochastic calculus context.

We show a class of stock price models with stochastic volatility for which the most natural candidates for martingale measures are only strictly local martingale measures, contrary to what is usually assumed in the finance literature. We also show the existence of equivalent martingale measures, and provide one explicit example.

Dynamic asset allocation strategies that are continuously rebalanced so as to always keep a fixed constant proportion of wealth invested in the various assets at each point in time play a fundamental role in the theory of optimal portfolio strategies. In this paper we study the rate of return on investment, defined here as the net gain in wealth divided by the cumulative investment, for such investment strategies in continuous time. Among other results, we prove that the limiting distribution of this measure of return is a gamma distribution. This limit theorem allows for comparisons of different strategies. For example, the mean return on investment is maximized by the same strategy that maximizes logarithmic utility, which is also known to maximize the exponential rate at which wealth grows. The return from this policy turns out to have other stochastic dominance properties as well. We also study the return on the risky investment alone, defined here as the present value of the gain from investment divided by the present value of the cumulative investment in the risky asset needed to achieve the gain. We show that for the log-optimal, or optimal growth policy, this return tends to an exponential distribution. We compare the return from the optimal growth policy with the return from a policy that invests a constant amount in the risky stock. We show that for the case of a single risky investment, the constant investor's expected return is twice that of the optimal growth policy. This difference can be considered the cost for insuring that the proportional investor does not go bankrupt.

In this paper we study the problem of pricing contingent claims for a large investor (i.e. the coefficients of the price equation can also depend on the wealth process of the hedger) in an incomplete market where the portfolios are constrained. We formulate this problem so as to find the minimal solution of forward-backward stochastic differential equations (FBSDEs) with constraints. We use the penalization method to construct a sequence of FBSDEs without constraints, and we show that the solutions of these equations converge to the minimal solution we are interested in.

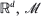In this paper we consider a position–velocity Ornstein-Uhlenbeck process in an external gradient force field pushing it toward a smoothly imbedded submanifold of . The force is chosen so that 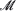is asymptotically stable for the associated deterministic flow. We examine the asymptotic behavior of the system when the force intensity diverges together with the diffusion and the damping coefficients, with appropriate speed. We prove that, under some natural conditions on the initial data, the sequence of position processes is relatively compact, any limit process is constrained on 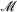, and satisfies an explicit stochastic differential equation which, for compact 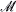, has a unique solution.

We consider a risk process with stochastic interest rate, and show that the probability of eventual ruin and the Laplace transform of the time of ruin can be found by solving certain boundary value problems involving integro-differential equations. These equations are then solved for a number of special cases. We also show that a sequence of such processes converges weakly towards a diffusion process, and analyze the above-mentioned ruin quantities for the limit process in some detail.

We consider a continuous polling system in heavy traffic. Using the relationship between such systems and age-dependent branching processes, we show that the steady-state number of waiting customers in heavy traffic has approximately a gamma distribution. Moreover, given their total number, the configuration of these customers is approximately deterministic.

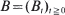The solution is presented to all optimal stopping problems of the form supτE(G(|Β τ |) – cτ), where is standard Brownian motion and the supremum is taken over all stopping times 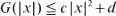τ for B with finite expectation, while the map G : ℝ+ → ℝ satisfies for some 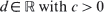being given and fixed. The optimal stopping time is shown to be the hitting time by the reflecting Brownian motion 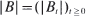of the set of all (approximate) maximum points of the map 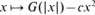. The method of proof relies upon Wald's identity for Brownian motion and simple real analysis arguments. A simple proof of the Dubins–Jacka–Schwarz–Shepp–Shiryaev (square root of two) maximal inequality for randomly stopped Brownian motion is given as an application.

In this article we study stochastic perturbations of partial differential equations describing forced-damped vibrations of a string. Two models of such stochastic disturbances are considered; one is triggered by an initial white noise, and the other is in the form of non-Gaussian random forcing. Let uε (t, x) be the displacement at time t of a point x on a string, where the time variable t ≧ 0, and the space variable . 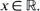The small parameter ε controls the intensity of the random fluctuations. The random fields uε (t, x) are shown to satisfy a large deviations principle, and the random deviations of the unperturbed displacement function are analyzed as the noise parameter ε tends to zero.

We study a classical stochastic control problem arising in financial economics: to maximize expected logarithmic utility from terminal wealth and/or consumption. The novel feature of our work is that the portfolio is allowed to anticipate the future, i.e. the terminal values of the prices, or of the driving Brownian motion, are known to the investor, either exactly or with some uncertainty. Results on the finiteness of the value of the control problem are obtained in various setups, using techniques from the so-called enlargement of filtrations. When the value of the problem is finite, we compute it explicitly and exhibit an optimal portfolio in closed form.

The paper introduces an approach focused towards the modelling of dynamics of financial markets. It is based on the three principles of market clearing, exclusion of instantaneous arbitrage and minimization of increase of arbitrage information. The last principle is equivalent to the minimization of the difference between the risk neutral and the real world probability measures. The application of these principles allows us to identify various market parameters, e.g. the risk-free rate of return. The approach is demonstrated on a simple financial market model, for which the dynamics of a virtual risk-free rate of return can be explicitly computed.

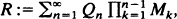We investigate the behaviour of P(R ≧ r) and P(R ≦ −r) as r → ∞for the random variable where 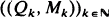is an independent, identically distributed sequence with P(− 1 ≦ M ≦ 1) = 1. Random variables of this type appear in insurance mathematics, as solutions of stochastic difference equations, in the analysis of probabilistic algorithms and elsewhere. Exponential and Poissonian tail behaviour can arise.

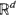We study the dispersion of a collection of particles carried by an isotropic Brownian flow in Of particular interest are the center of mass and the centered spatial second moments. Their asymptotic behavior depends strongly on the spatial dimension and the largest Lyapunov exponent of the flow. We use estimates for the pair separation process to give a fairly complete picture of this behavior as t → ∞. In particular, for incompressible flows in two dimensions, we show that the variance of the center of mass grows sublinearly, while dispersion relative to the center of mass grows linearly.

A Cox risk process with a piecewise constant intensity is considered where the sequence (Li ) of successive levels of the intensity forms a Markov chain. The duration σi of the level Li is assumed to be only dependent via Li . In the small-claim case a Lundberg inequality is obtained via a martingale approach. It is shown furthermore by a Lundberg bound from below that the resulting adjustment coefficient gives the best possible exponential bound for the ruin probability. In the case where the stationary distribution of Li contains a discrete component, a Cramér–Lundberg approximation can be obtained. By way of example we consider the independent jump intensity model (Björk and Grandell 1988) and the risk model in a Markovian environment (Asmussen 1989).

We study the limiting behaviour of large systems of two types of Brownian particles undergoing bisexual branching. Particles of each type generate individuals of both types, and the respective branching law is asymptotically critical for the two-dimensional system, while being subcritical for each individual population.

The main result of the paper is that the limiting behaviour of suitably scaled sums and differences of the two populations is given by a pair of measure and distribution valued processes which, together, determine the limit behaviours of the individual populations.

Our proofs are based on the martingale problem approach to general state space processes. The fact that our limit involves both measure and distribution valued processes requires the development of some new methodologies of independent interest.