Refine listing
Actions for selected content:
333 results in 60Hxx
Implicit Renewal Theory and Power Tails on Trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 528-561
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Almost sure asymptotic stability analysis of the θ-Maruyama method applied to a test system with stabilising and destabilising stochastic perturbations
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 April 2012, pp. 71-83
-
- Article
-
- You have access
- Export citation
ASYMPTOTIC BEHAVIOUR OF RANDOM MARKOV CHAINS WITH TRIDIAGONAL GENERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 30 March 2012, pp. 27-36
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
Dimension reduction and homogenization of random degenerate operators. Part I
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 January 2012, pp. 1-22
-
- Article
-
- You have access
- Export citation
CONVOLUTION OF FUNCTIONALS OF DISCRETE-TIME NORMAL MARTINGALES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 16 December 2011, pp. 224-231
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Tail behavior of multivariate lévy-driven mixed moving average processes and supOU Stochastic Volatility Models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1109-1135
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Efficient nonlinear filtering of a singularly perturbed stochastic hybrid system
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 November 2011, pp. 254-270
-
- Article
-
- You have access
- Export citation
A Note on a Paper by Wong and Heyde
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 811-819
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Volatility determination in an ambit process setting
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue A / August 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 263-275
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
On the ruin probability of the generalised Ornstein–Uhlenbeck process in the cramér case
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue A / August 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 15-28
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
A piecewise linear stochastic differential equation driven by a Lévy process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue A / August 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 109-119
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
Optimal control of stochastic delay equations and time-advanced backward stochastic differential equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 572-596
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
COHERENT STATES IN BERNOULLI NOISE FUNCTIONALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 01 April 2011, pp. 116-126
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
Information: price and impact on general welfare and optimal investment. an anticipative stochastic differential game model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 97-120
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
On Tails of Perpetuities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1191-1194
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Information ranking and power laws on trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1057-1093
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
An optimal portfolio problem in a defaultable market
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 689-705
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
A general comparison theorem for backward stochastic differential equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 878-898
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Stochastic Integrals and Conditional Full Support
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 650-667
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Mean reversion for HJMM forward rate models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 371-391
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
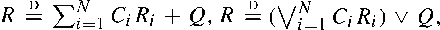 and similar recursions, where (
and similar recursions, where (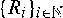 are independent and identically distributed copies of
are independent and identically distributed copies of 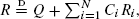 where
where 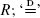 stands for equality in distribution. We study the asymptotic properties of the distribution of
stands for equality in distribution. We study the asymptotic properties of the distribution of 