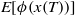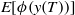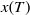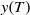Refine listing
Actions for selected content:
333 results in 60Hxx
On Optimal Retirement
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 333-345
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
STATISTICAL CAUSALITY AND MARTINGALE REPRESENTATION PROPERTY WITH APPLICATION TO STOCHASTIC DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 20 May 2014, pp. 327-338
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Conditional Characteristic Functions of Molchan-Golosov Fractional Lévy Processes with Application to Credit Risk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 983-1005
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Convergence Rates in the Implicit Renewal Theorem on Trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1077-1088
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Weak approximation of stochastic differential delay equations for bounded measurable function
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 September 2013, pp. 319-343
-
- Article
-
- You have access
- Export citation
On the Dynamics of Semimartingales with Two Reflecting Barriers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 671-685
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
Discrete-Time Approximation of Decoupled Forward‒Backward Stochastic Differential Equations Driven by Pure Jump Lévy Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 791-821
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
Corrigendum: On the use of a discrete form of the Itô formula in the article ‘Almost sure asymptotic stability analysis of the
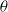 $\theta $ -Maruyama method applied to a test system with stabilising and destabilising stochastic perturbations’
$\theta $ -Maruyama method applied to a test system with stabilising and destabilising stochastic perturbations’
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 September 2013, pp. 366-372
-
- Article
-
- You have access
- Export citation
Probabilistic Methods for the Incompressible Navier–Stokes Equations With Space Periodic Conditions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 742-772
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
Useful Martingales for Stochastic Storage Processes with Lévy-Type Input
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 439-449
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Cross-Commodity Spot Price Modeling with Stochastic Volatility and Leverage For Energy Markets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 22 February 2016, pp. 545-571
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Pricing of Forwards and Options in a Multivariate Non-Gaussian Stochastic Volatility Model for Energy Markets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 22 February 2016, pp. 572-594
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Conditional Distributions of Processes Related to Fractional Brownian Motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 1 / March 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 166-183
- Print publication:
- March 2013
-
- Article
-
- You have access
- Export citation
Optimal Design of Dynamic Default Risk Measures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 30 January 2018, pp. 967-977
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Functional Relationships Between Price and Volatility Jumps and Their Consequences for Discretely Observed Data
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 30 January 2018, pp. 901-914
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
On the Exponential Ergodicity of Lévy-Driven Ornstein–Uhlenbeck Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 30 January 2018, pp. 990-1004
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Convex Duality in Mean-Variance Hedging Under Convex Trading Constraints
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 1084-1112
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
EQUATIONS WITH DIRICHLET BOUNDARY NOISE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 31 October 2012, pp. 174-176
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
On the Optimal Dividend Strategy in a Regime-Switching Diffusion Model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 886-906
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
First Passage Time of Skew Brownian Motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 685-696
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation