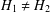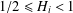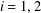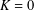Refine listing
Actions for selected content:
337 results in 60Hxx
On perpetuities with gamma-like tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 368-389
- Print publication:
- June 2018
-
- Article
- Export citation
Uniqueness for measure-valued equations of nonlinear filtering for stochastic dynamical systems with Lévy noise
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 396-413
- Print publication:
- June 2018
-
- Article
- Export citation
Joint distribution of a Lévy process and its running supremum
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 488-512
- Print publication:
- June 2018
-
- Article
- Export citation
An optimal consumption and investment problem with partial information
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 131-153
- Print publication:
- March 2018
-
- Article
-
- You have access
- Export citation
Conjugate duality in stochastic controls with delay
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 17 November 2017, pp. 1011-1036
- Print publication:
- December 2017
-
- Article
- Export citation
Itô-Taylor Schemes for Solving Mean-Field Stochastic Differential Equations
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 12 September 2017, pp. 798-828
- Print publication:
- November 2017
-
- Article
- Export citation
Implicit renewal theory in the arithmetic case
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 732-749
- Print publication:
- September 2017
-
- Article
- Export citation
Large deviation principle for epidemic models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 905-920
- Print publication:
- September 2017
-
- Article
- Export citation
Optimal Error Estimates for a Fully Discrete Euler Scheme for Decoupled Forward Backward Stochastic Differential Equations
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 07 September 2017, pp. 548-565
- Print publication:
- August 2017
-
- Article
- Export citation
SHORT TIME FULL ASYMPTOTIC EXPANSION OF HYPOELLIPTIC HEAT KERNEL AT THE CUT LOCUS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 10 July 2017, e16
-
- Article
-
- You have access
- Open access
- Export citation
Second-order differential equations with random perturbations and small parameters
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 05 July 2017, pp. 763-779
- Print publication:
- August 2017
-
- Article
- Export citation
On the large-time behaviour of the solution of a stochastic differential equation driven by a Poisson point process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 26 June 2017, pp. 344-367
- Print publication:
- June 2017
-
- Article
- Export citation
Large deviations for the stochastic predator–prey model with nonlinear functional response
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 22 June 2017, pp. 507-521
- Print publication:
- June 2017
-
- Article
- Export citation
ON MULTI-ASSET SPREAD OPTION PRICING IN A WICK–ITÔ–SKOROHOD INTEGRAL FRAMEWORK
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 24 May 2017, pp. 386-396
-
- Article
-
- You have access
- Export citation
Deferred Correction Methods for Forward Backward Stochastic Differential Equations
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 May 2017, pp. 222-242
- Print publication:
- May 2017
-
- Article
- Export citation
RARE EVENTS IN THE STOCHASTIC CAMASSA–HOLM EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 06 March 2017, pp. 417-427
-
- Article
-
- You have access
- Export citation
High Order Numerical Schemes for Second-Order FBSDEs with Applications to Stochastic Optimal Control
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 07 February 2017, pp. 808-834
- Print publication:
- March 2017
-
- Article
- Export citation
A Compact Scheme for Coupled Stochastic Nonlinear Schrödinger Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 93-125
- Print publication:
- January 2017
-
- Article
- Export citation
Construction of Symplectic Runge-Kutta Methods for Stochastic Hamiltonian Systems
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 237-270
- Print publication:
- January 2017
-
- Article
- Export citation
Distributions of jumps in a continuous-state branching process with immigration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1166-1177
- Print publication:
- December 2016
-
- Article
- Export citation