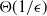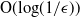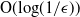Refine listing
Actions for selected content:
337 results in 60Hxx
Optimal multiple stopping problem under nonlinear expectation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 September 2022, pp. 151-178
- Print publication:
- March 2023
-
- Article
- Export citation
Impacts of noise on quenching of some models arising in MEMS technology
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 09 August 2022, pp. 1209-1241
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rate of convergence for particle approximation of PDEs in Wasserstein space
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 28 July 2022, pp. 992-1008
- Print publication:
- December 2022
-
- Article
- Export citation
Mutually interacting superprocesses with migration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 July 2022, pp. 904-929
- Print publication:
- September 2022
-
- Article
- Export citation
Logarithmic heavy traffic error bounds in generalized switch and load balancing systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 June 2022, pp. 652-669
- Print publication:
- September 2022
-
- Article
- Export citation
Extended reduced-form framework for non-life insurance
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 945-973
- Print publication:
- September 2022
-
- Article
- Export citation
Optimal consumption with Hindy–Huang–Kreps preferences under nonlinear expectations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1222-1251
- Print publication:
- December 2022
-
- Article
- Export citation
On operator fractional Lévy motion: integral representations and time-reversibility
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 493-535
- Print publication:
- June 2022
-
- Article
- Export citation
Construction of age-structured branching processes by stochastic equations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 31 May 2022, pp. 670-684
- Print publication:
- September 2022
-
- Article
-
- You have access
- HTML
- Export citation
Probabilistic analysis of replicator–mutator equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 23 March 2022, pp. 167-201
- Print publication:
- March 2022
-
- Article
- Export citation
Convergence rate of the EM algorithm for SDEs with low regular drifts
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 14 February 2022, pp. 447-470
- Print publication:
- June 2022
-
- Article
- Export citation
The support of singular stochastic partial differential equations
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 14 January 2022, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exact simulation of coupled Wright–Fisher diffusions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 923-950
- Print publication:
- December 2021
-
- Article
- Export citation
Large deviation principles of 2D stochastic Navier–Stokes equations with Lévy noises
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 18 November 2021, pp. 19-67
- Print publication:
- February 2023
-
- Article
- Export citation
Diffusion approximation of multi-class Hawkes processes: Theoretical and numerical analysis
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 716-756
- Print publication:
- September 2021
-
- Article
- Export citation
Exact simulation of Ornstein–Uhlenbeck tempered stable processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 347-371
- Print publication:
- June 2021
-
- Article
- Export citation
Weak convergence of stochastic integrals with respect to the state occupation measure of a Markov chain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 372-393
- Print publication:
- June 2021
-
- Article
- Export citation
INVESTIGATING ATTRIBUTE RISKS AND CONSTRUCTING LINKAGE ERROR MODELS FOR PROBABILISTICALLY-LINKED DATA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 19 April 2021, pp. 346-348
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
Self-exciting multifractional processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 22-41
- Print publication:
- March 2021
-
- Article
- Export citation
Generalised liouville processes and their properties
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1088-1110
- Print publication:
- December 2020
-
- Article
- Export citation