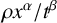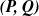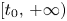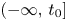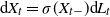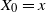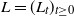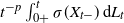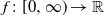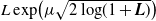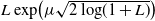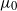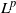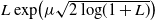Refine listing
Actions for selected content:
337 results in 60Hxx
SUPPORT THEOREM FOR PINNED DIFFUSION PROCESSES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 241-264
- Print publication:
- March 2024
-
- Article
- Export citation
Heavy-traffic limits for parallel single-server queues with randomly split Hawkes arrival processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 07 August 2023, pp. 490-514
- Print publication:
- June 2024
-
- Article
- Export citation
Duality theory for exponential utility-based hedging in the Almgren–Chriss model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 03 August 2023, pp. 420-438
- Print publication:
- June 2024
-
- Article
- Export citation
PDE for the joint law of the pair of a continuous diffusion and its running maximum
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 10 July 2023, pp. 1171-1210
- Print publication:
- December 2023
-
- Article
- Export citation
Weakly interacting oscillators on dense random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 30 June 2023, pp. 255-278
- Print publication:
- March 2024
-
- Article
- Export citation
PRICING AND HEDGING OF VIX DERIVATIVES IN MODIFIED STOCHASTIC MODELS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 23 June 2023, pp. 351-352
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
CONDITIONS FOR RECURRENCE AND TRANSIENCE FOR TIME-INHOMOGENEOUS BIRTH-AND-DEATH PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 393-402
- Print publication:
- April 2024
-
- Article
- Export citation
ESSAYS ON STRONG AND WEAK APPROXIMATIONS OF STOCHASTIC DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 175-176
- Print publication:
- August 2023
-
- Article
-
- You have access
- HTML
- Export citation
Explosion of continuous-state branching processes with competition in a Lévy environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 09 June 2023, pp. 68-81
- Print publication:
- March 2024
-
- Article
- Export citation
Measuring the suboptimality of dividend controls in a Brownian risk model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 07 June 2023, pp. 1442-1472
- Print publication:
- December 2023
-
- Article
- Export citation
Averaging for slow–fast piecewise deterministic Markov processes with an attractive boundary
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 19 May 2023, pp. 1439-1468
- Print publication:
- December 2023
-
- Article
- Export citation
Exponential control of the trajectories of iterated function systems with application to semi-strong GARCH
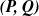 $\boldsymbol{{(P, Q)}}$ models
$\boldsymbol{{(P, Q)}}$ models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1501-1515
- Print publication:
- December 2023
-
- Article
- Export citation
Fluctuations for Some Nonstationary Interacting Particle Systems via Boltzmann–Gibbs Principle
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 25 April 2023, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Robustness of nonuniform mean-square exponential dichotomies
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 18 April 2023, pp. 525-567
- Print publication:
- April 2024
-
- Article
- Export citation
Strong feller and ergodic properties of the (1+1)-affine process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 14 March 2023, pp. 812-834
- Print publication:
- September 2023
-
- Article
- Export citation
Sandwiched SDEs with unbounded drift driven by Hölder noises
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 08 March 2023, pp. 927-964
- Print publication:
- September 2023
-
- Article
- Export citation
Short-time behavior of solutions to Lévy-driven stochastic differential equations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 765-780
- Print publication:
- September 2023
-
- Article
- Export citation
On mixed fractional stochastic differential equations with discontinuous drift coefficient
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 01 December 2022, pp. 589-606
- Print publication:
- June 2023
-
- Article
- Export citation
Brownian bridge expansions for Lévy area approximations and particular values of the Riemann zeta function
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 03 November 2022, pp. 370-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal stopping under g-Expectation with
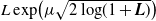 ${L}\exp\bigl(\mu\sqrt{2\log\!(1+\textbf{L})}\bigr)$-integrable reward process
${L}\exp\bigl(\mu\sqrt{2\log\!(1+\textbf{L})}\bigr)$-integrable reward process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 14 September 2022, pp. 241-252
- Print publication:
- March 2023
-
- Article
- Export citation