Motivated by a problem in neural encoding, we introduce an adaptive (or real-time) parameter estimation algorithm driven by a counting process. Despite the long history of adaptive algorithms, this kind of algorithm is relatively new. We develop a finite-time averaging analysis which is nonstandard partly because of the point process setting and partly because we have sought to avoid requiring mixing conditions. This is significant since mixing conditions often place restrictive history-dependent requirements on algorithm convergence.

The inability to predict the future growth rates and earnings of growth stocks (such as biotechnology and internet stocks) leads to the high volatility of share prices and difficulty in applying the traditional valuation methods. This paper attempts to demonstrate that the high volatility of share prices can nevertheless be used in building a model that leads to a particular cross-sectional size distribution. The model focuses on both transient and steady-state behavior of the market capitalization of the stock, which in turn is modeled as a birth-death process. Numerical illustrations of the cross-sectional size distribution are also presented.

Upper as well as lower bounds for both the large deviations and small deviations of several sup-norms associated with the displacements of a one-dimensional string driven by a Gaussian noise which is white in time and has general spatial covariance are developed.

We study the existence of moments and the tail behavior of the densities of storage processes. We give sufficient conditions for existence and nonexistence of moments using the integrability conditions of submultiplicative functions with respect to Lévy measures. We then study the asymptotical behavior of the tails of these processes using the concave or convex envelope of the release rate function.

We study linear jump parameter systems of differential and difference equations whose coefficients depend on the state of a semi-Markov process. We derive systems of equations for the first two moments of the random solutions of these jump parameter systems, and illustrate how moment equations can be used in examining their asymptotic stability.

We first give the existence and uniqueness result and a comparison theorem for backward stochastic differential equations with Brownian motion and Poisson process as the noise source in stopping time (unbounded) duration. Then we obtain the existence and uniqueness result for fully coupled forward-backward stochastic differential equation with Brownian motion and Poisson process in stopping time (unbounded) duration. We also proved a comparison theorem for this kind of equation.

In this paper, the class of periodic Ornstein-Uhlenbeck processes is defined. It is shown that periodic Ornstein-Uhlenbeck processes are stationary Markov random fields and the class of stationary distributions is characterized. In particular, any self-decomposable distribution is the stationary distribution of some periodic Ornstein-Uhlenbeck process. As examples, gamma periodic Ornstein-Uhlenbeck processes and Gaussian periodic Ornstein-Uhlenbeck processes are considered.

Consider a real-valued Itô process X(t) = x + ∫0tμ(s)ds + ∫0tσ(s)dW(s) + A(t) driven by a Brownian motion {W(t) : t > 0}. The controller chooses the real-valued progressively measurable processes μ, σ and A subject to constraints |μ(t)| ≤ μ0(X(t-)) and |σ(t)| ≥ σ0(X(t-)), where the functions μ0 and σ0 are given. The process A is a bounded variation process and |A|(t) represents its total variation on [0,t]. The objective is to minimize the long-term average cost lim supT→∞(1/T)E[|A|(T) + ∫0Th(X(s))ds], where h is a given nonnegative continuous function. An optimal process X* is determined. It turned out that X* is a reflecting diffusion process whose state space is a finite interval [a*, b*]. The optimal drift and diffusion controls are explicitly derived and the optimal bounded variation process A* is determined in terms of local-time processes of X* at the points a* and b*.

In this paper we consider the stochastic wave equation in one spatial dimension driven by a two-parameter Gaussian noise which is white in time and has general spatial covariance. We give conditions on the spatial covariance of the driving noise sufficient for the string to have finite expected energy and calculate this energy as a function of time. We show that these same conditions on the spatial covariance of the driving noise are also sufficient to guarantee that the energy of the string has a version which is continuous almost surely.

We solve the following three optimal stopping problems for different kinds of options, based on the Black-Scholes model of stock fluctuations. (i) The perpetual lookback American option for the running maximum of the stock price during the life of the option. This problem is more difficult than the closely related one for the Russian option, and we show that for a class of utility functions the free boundary is governed by a nonlinear ordinary differential equation. (ii) A new type of stock option, for a company, where the company provides a guaranteed minimum as an added incentive in case the market appreciation of the stock is low, thereby making the option more attractive to the employee. We show that the value of this option is given by solving a nonalgebraic equation. (iii) A new call option for the option buyer who is risk-averse and gets to choose, a priori, a fixed constant l as a ‘hedge’ on a possible downturn of the stock price, where the buyer gets the maximum of l and the price at any exercise time. We show that the optimal policy depends on the ratio of x/l, where x is the current stock price.

We study the last passage time and its asymptotic distribution for minimum contrast estimators defined through the minimization of a convex criterion function based on U-functionals. This includes cases of non-smooth estimators for vector valued parameters. We also derive a Bahadur-type representation and the law of iterated logarithms for such estimators.

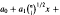
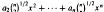An asymptotic estimate is derived for the expected number of extrema of a polynomial whose independent normal coefficients possess non-equal non-zero mean values. A result is presented that generalizes in terms of normal processes the analytical device used for construction of similar asymptotic estimates for random polynomials with normal coefficients.

A new representation for the characteristic function of the multivariate strictly geo-stable distribution is presented. The representation is appealing from a parametric viewpoint: its parameters have an intuitive probabilistic interpretation; and it is particularly useful for estimating the parameters of the geo-stable distribution.

We provide a set of verifiable sufficient conditions for proving in a number of practical examples the equivalence of the martingale and the PDE approaches to the valuation of derivatives. The key idea is to use a combination of analytic and probabilistic assumptions that covers typical models in finance falling outside the range of standard results from the literature. Applications include Heston's stochastic volatility model and the Black-Karasinski term structure model.

The maximality principle [6] is shown to be valid in some examples of discounted optimal stopping problems for the maximum process. In each of these examples explicit formulas for the value functions are derived and the optimal stopping times are displayed. In particular, in the framework of the Black-Scholes model, the fair prices of two lookback options with infinite horizon are calculated. The main aim of the paper is to show that in each considered example the optimal stopping boundary satisfies the maximality principle and that the value function can be determined explicitly.

In this paper, we first give a sufficient condition on the coefficients of a class of infinite time interval backward stochastic differential equations (BSDEs) under which the infinite time interval BSDEs have a unique solution for any given square integrable terminal value, and then, using the infinite time interval BSDEs, we study the convergence of g-martingales introduced by Peng via a kind of BSDEs. Finally, we study the applications of g-expectations and g-martingales in both finance and economics.

We consider a probabilistic model of a heterogeneous population P subdivided into homogeneous sub-cohorts. A main assumption is that the frailties give rise to a discrete, exchangeable random vector. We put ourselves in the framework of stochastic filtering to derive the conditional distribution of residual lifetimes of surviving individuals, given an observed history of failures and survivals. As a main feature of our approach, this study is based on the analysis of behaviour of the vector of ‘occupation numbers’.

We define a class of anticipative flows on Poisson space and compute its Radon-Nikodym derivative. This result is applied to statistical testing in an anticipative queueing problem.

In various stochastic models the random equation of implicit renewal theory appears where the real random variable S and the stochastic process Ψ with index space and state space R are independent. By use of stochastic approximation the distribution function of S is recursively estimated on the basis of independent or ergodic copies of Ψ. Under integrability assumptions almost sure L1-convergence is proved. The choice of gains in the recursion is discussed. Applications are given to insurance mathematics (perpetuities) and queueing theory (stationary waiting and queueing times).

Let Xt be a Feller (branching) diffusion with drift αx. We consider new processes, the probability measures of which are obtained from that of X via changes of measure involving suitably normalized exponential functions of with λ > 0. The new processes can be thought of as ‘self-reinforcing’ versions of the old.

Depending on the values of α, T and λ, the process under the new measure is shown to exhibit explosion in finite time. We also obtain a number of other results related to the new processes.

Since the Feller diffusion is also the total mass process of a superprocess, we relate the finite-time explosion property to the behaviour of superprocesses with local self-interaction, and raise some interesting questions for these.