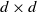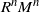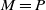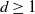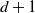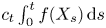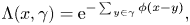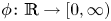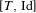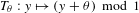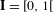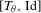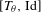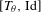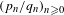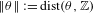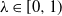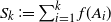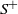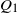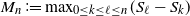Refine listing
Actions for selected content:
1723 results in 60Jxx
Out-of-equilibrium random walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 772-797
- Print publication:
- September 2020
-
- Article
- Export citation
Stochastically modeled weakly reversible reaction networks with a single linkage class
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 792-810
- Print publication:
- September 2020
-
- Article
- Export citation
Ergodicity of affine processes on the cone of symmetric positive semidefinite matrices
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 825-854
- Print publication:
- September 2020
-
- Article
- Export citation
Perron–Frobenius theory for kernels and Crump–Mode–Jagers processes with macro-individuals
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 720-733
- Print publication:
- September 2020
-
- Article
- Export citation
Mixing and average mixing times for general Markov processes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 14 August 2020, pp. 541-552
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
Approximately counting bases of bicircular matroids
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 06 August 2020, pp. 124-135
-
- Article
- Export citation
Heavy-tailed branching random walks on multidimensional lattices. A moment approach
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 22 July 2020, pp. 971-992
- Print publication:
- June 2021
-
- Article
- Export citation
On a class of random walks in simplexes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 409-428
- Print publication:
- June 2020
-
- Article
- Export citation
Tails of exit times from unstable equilibria on the line
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 477-496
- Print publication:
- June 2020
-
- Article
- Export citation
Joint law of an Ornstein–Uhlenbeck process and its supremum
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 541-558
- Print publication:
- June 2020
-
- Article
- Export citation
Limit theorems for sequential MCMC methods
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 377-403
- Print publication:
- June 2020
-
- Article
- Export citation
Optimal stopping for measure-valued piecewise deterministic Markov processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 497-512
- Print publication:
- June 2020
-
- Article
- Export citation
Mean reflected stochastic differential equations with jumps
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 523-562
- Print publication:
- June 2020
-
- Article
- Export citation
Limit theorems for additive functionals of continuous time random walks
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 28 May 2020, pp. 799-820
- Print publication:
- April 2021
-
- Article
- Export citation
The size of the primes obstructing the existence of rational points
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 15 May 2020, pp. 652-704
- Print publication:
- April 2021
-
- Article
- Export citation
Bernoulliness of
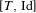 $[T,\text{Id}]$ when
$[T,\text{Id}]$ when  $T$ is an irrational rotation: towards an explicit isomorphism
$T$ is an irrational rotation: towards an explicit isomorphism
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 24 April 2020, pp. 2110-2135
- Print publication:
- July 2021
-
- Article
- Export citation
Integral functionals under the excursion measure
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 137-155
- Print publication:
- March 2020
-
- Article
- Export citation
An invariance principle and a large deviation principle for the biased random walk on
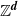 ${\mathbb{Z}}^{\lowercase{\textbf{\textit{d}}}}$
${\mathbb{Z}}^{\lowercase{\textbf{\textit{d}}}}$
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 295-313
- Print publication:
- March 2020
-
- Article
- Export citation
Long-time behavior of Lévy-driven Ornstein–Uhlenbeck processes with regime switching
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 266-279
- Print publication:
- March 2020
-
- Article
- Export citation
Improvements on the distribution of maximal segmental scores in a Markovian sequence
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 29-52
- Print publication:
- March 2020
-
- Article
- Export citation