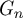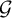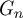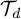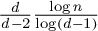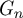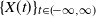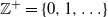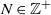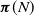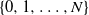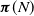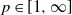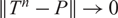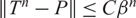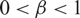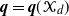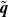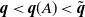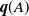Refine listing
Actions for selected content:
1723 results in 60Jxx
CUTOFF AT THE ENTROPIC TIME FOR RANDOM WALKS ON COVERED EXPANDER GRAPHS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 09 February 2021, pp. 1571-1616
- Print publication:
- September 2022
-
- Article
- Export citation
Postponing production exponentially enhances the molecular memory of a stochastic switch
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 12 January 2021, pp. 182-199
-
- Article
- Export citation
Large deviations for a class of tempered subordinators and their inverse processes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 2030-2050
- Print publication:
- December 2021
-
- Article
- Export citation
Limit theorems for multi-type general branching processes with population dependence
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1127-1163
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
Corrigendumto: Asymptotic shape and the speed of propagation of continuous-time continuous-space birth processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1325-1327
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
Characterization of the conditional stationary distribution in Markov chains via systems of linear inequalities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1249-1283
- Print publication:
- December 2020
-
- Article
- Export citation
Draw-down Parisian ruin for spectrally negative Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1164-1196
- Print publication:
- December 2020
-
- Article
- Export citation
Multivariate finite-support phase-type distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1260-1275
- Print publication:
- December 2020
-
- Article
- Export citation
Rate of convergence for traditional Pólya urns
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1029-1044
- Print publication:
- December 2020
-
- Article
- Export citation
Generalised liouville processes and their properties
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1088-1110
- Print publication:
- December 2020
-
- Article
- Export citation
On geometric and algebraic transience for block-structured Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1313-1338
- Print publication:
- December 2020
-
- Article
- Export citation
The empirical mean position of a branching Lévy process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1252-1259
- Print publication:
- December 2020
-
- Article
- Export citation
Skeletal stochastic differential equations for superprocesses
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1111-1134
- Print publication:
- December 2020
-
- Article
- Export citation
Spread out random walks on homogeneous spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 06 October 2020, pp. 3439-3473
- Print publication:
- November 2021
-
- Article
- Export citation
Markov chains with exponential return times are finitary
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 29 September 2020, pp. 2918-2926
- Print publication:
- October 2021
-
- Article
- Export citation
SPECTRAL CONDITIONS FOR UNIFORM P-ERGODICITIES OF MARKOV OPERATORS ON ABSTRACT STATES SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 23 September 2020, pp. 682-696
- Print publication:
- September 2021
-
- Article
- Export citation
Coarse graining of a Fokker–Planck equation with excluded volume effects preserving the gradient flow structure
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 22 September 2020, pp. 711-745
-
- Article
-
- You have access
- Open access
- Export citation
On the policy improvement algorithm for ergodic risk-sensitive control
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 02 September 2020, pp. 1305-1330
- Print publication:
- August 2021
-
- Article
- Export citation
The probabilities of extinction in a branching random walk on a strip
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 811-831
- Print publication:
- September 2020
-
- Article
- Export citation
On branching models with alarm triggerings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 734-759
- Print publication:
- September 2020
-
- Article
- Export citation