Refine listing
Actions for selected content:
1723 results in 60Jxx
Skeletal stochastic differential equations for continuous-state branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 11 December 2019, pp. 1122-1150
- Print publication:
- December 2019
-
- Article
- Export citation
Asymptotic variance for random walk Metropolis chains in high dimensions: logarithmic growth via the Poisson equation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 November 2019, pp. 994-1026
- Print publication:
- December 2019
-
- Article
- Export citation
Exact sampling for some multi-dimensional queueing models with renewal input
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 November 2019, pp. 1179-1208
- Print publication:
- December 2019
-
- Article
- Export citation
Insensitivity of the mean field limit of loss systems under SQ(d) routeing
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 November 2019, pp. 1027-1066
- Print publication:
- December 2019
-
- Article
- Export citation
On the ergodicity of a class of level-dependent quasi-birth-and-death processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 November 2019, pp. 1109-1128
- Print publication:
- December 2019
-
- Article
- Export citation
Efficient simulation of Lévy-driven point processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 November 2019, pp. 927-966
- Print publication:
- December 2019
-
- Article
- Export citation
COVER TIME FOR THE FROG MODEL ON TREES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 08 November 2019, e41
-
- Article
-
- You have access
- Open access
- Export citation
Non-triviality of the Poisson boundary of random walks on the group
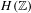 $H(\mathbb{Z})$ of Monod
$H(\mathbb{Z})$ of Monod
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 04 November 2019, pp. 1160-1189
- Print publication:
- April 2021
-
- Article
- Export citation
SMALL-WORLD EFFECT IN GEOGRAPHICAL ATTACHMENT NETWORKS
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 35 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 12 September 2019, pp. 276-296
-
- Article
- Export citation
Approximate lumpability for Markovian agent-based models using local symmetries
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 647-671
- Print publication:
- September 2019
-
- Article
- Export citation
On first exit times and their means for Brownian bridges
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 701-722
- Print publication:
- September 2019
-
- Article
- Export citation
Branching Brownian motion with spatially homogeneous and point-catalytic branching
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 891-917
- Print publication:
- September 2019
-
- Article
- Export citation
Accelerating parallel tempering: Quantile tempering algorithm (QuanTA)
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 September 2019, pp. 802-834
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
WEAK SUBORDINATION OF MULTIVARIATE LÉVY PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 09 July 2019, pp. 518-519
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
UNIQUENESS OF THE WELDING PROBLEM FOR SLE AND LIOUVILLE QUANTUM GRAVITY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 05 July 2019, pp. 757-783
- Print publication:
- May 2021
-
- Article
- Export citation
Logarithmic Sobolev inequalities in discrete product spaces
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 13 June 2019, pp. 919-935
-
- Article
- Export citation
Extremes of multitype branching random walks: heaviest tail wins
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 514-540
- Print publication:
- June 2019
-
- Article
- Export citation
On association and other forms of positive dependence for Feller processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 624-646
- Print publication:
- June 2019
-
- Article
- Export citation
A martingale view of Blackwell’s renewal theorem and its extensions to a general counting process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 602-623
- Print publication:
- June 2019
-
- Article
- Export citation
Some explicit results on one kind of sticky diffusion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 398-415
- Print publication:
- June 2019
-
- Article
- Export citation
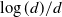
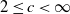
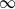







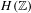
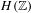
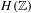
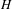
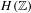


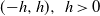
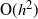
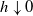

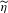
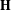

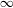


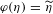


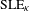
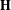

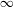

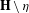
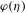


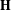

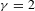
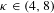
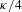
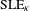
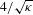
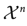 , (
, (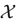 is a finite set), and any probability measure
is a finite set), and any probability measure 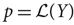 on
on