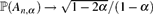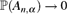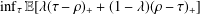Refine listing
Actions for selected content:
1723 results in 60Jxx
Assouad Dimension of Random Processes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 16 November 2018, pp. 281-290
-
- Article
- Export citation
DETECTION OF LONGITUDINAL BRAIN ATROPHY PATTERNS CONSISTENT WITH PROGRESSION TOWARDS ALZHEIMER’S DISEASE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 174-176
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Polynomial Mixing of the Edge-Flip Markov Chain for Unbiased Dyadic Tilings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 31 October 2018, pp. 365-387
-
- Article
- Export citation
Parking on a Random Tree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 23 October 2018, pp. 23-45
-
- Article
- Export citation
OPTIMAL STOPPING FOR THE LAST EXIT TIME
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 04 October 2018, pp. 148-160
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
THE FRIENDSHIP PARADOX FOR WEIGHTED AND DIRECTED NETWORKS
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 33 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 18 September 2018, pp. 136-145
-
- Article
- Export citation
Approximation of excessive backlog probabilities of two tandem queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 968-997
- Print publication:
- September 2018
-
- Article
- Export citation
Pair correlation functions and limiting distributions of iterated cluster point processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 789-809
- Print publication:
- September 2018
-
- Article
- Export citation
Importance sampling of heavy-tailed iterated random functions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 805-832
- Print publication:
- September 2018
-
- Article
- Export citation
Multi-type branching processes with time-dependent branching rates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 701-727
- Print publication:
- September 2018
-
- Article
- Export citation
Stochastic LU factorizations, Darboux transformations and urn models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 862-886
- Print publication:
- September 2018
-
- Article
- Export citation
Infinite-server queues with Hawkes input
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 920-943
- Print publication:
- September 2018
-
- Article
- Export citation
On an optimal extraction problem with regime switching
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 671-705
- Print publication:
- September 2018
-
- Article
- Export citation
Windings of planar processes, exponential functionals and Asian options
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 726-742
- Print publication:
- September 2018
-
- Article
- Export citation
Characterization and simplification of optimal strategies in positive stochastic games
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 728-741
- Print publication:
- September 2018
-
- Article
- Export citation
Integral estimation based on Markovian design
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 833-857
- Print publication:
- September 2018
-
- Article
- Export citation
NETWORKS OF INTERACTING STOCHASTIC FLUID MODELS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 30 August 2018, pp. 516-517
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Self-normalized large deviation for supercritical branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 450-458
- Print publication:
- June 2018
-
- Article
- Export citation
Spectral bounds in random graphs applied to spreading phenomena and percolation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 480-503
- Print publication:
- June 2018
-
- Article
- Export citation
Stochastic nonzero-sum games: a new connection between singular control and optimal stopping
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 347-372
- Print publication:
- June 2018
-
- Article
- Export citation