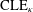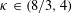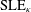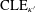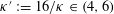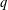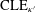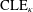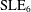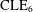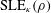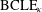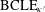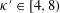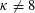Refine listing
Actions for selected content:
1723 results in 60Jxx
Forward sensitivity analysis for contracting stochastic systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 102-130
- Print publication:
- March 2018
-
- Article
- Export citation
Null recurrence and transience of random difference equations in the contractive case
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1089-1110
- Print publication:
- December 2017
-
- Article
- Export citation
Phase transition in random distance graphs on the torus
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1278-1294
- Print publication:
- December 2017
-
- Article
- Export citation
Note on discounted continuous-time Markov decision processes with a lower bounding function
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1071-1088
- Print publication:
- December 2017
-
- Article
- Export citation
A non-local random walk on the hypercube
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 17 November 2017, pp. 1288-1299
- Print publication:
- December 2017
-
- Article
- Export citation
Exponential ergodicity of an affine two-factor model based on the α-root process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 17 November 2017, pp. 1144-1169
- Print publication:
- December 2017
-
- Article
- Export citation
Fluid limit for the Poisson encounter-mating model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 17 November 2017, pp. 1201-1229
- Print publication:
- December 2017
-
- Article
- Export citation
MULTIPLICATIVELY CLOSED MARKOV MODELS MUST FORM LIE ALGEBRAS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 23 October 2017, pp. 240-246
-
- Article
-
- You have access
- Export citation
CLE PERCOLATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 5 / 2017
- Published online by Cambridge University Press:
- 03 October 2017, e4
-
- Article
-
- You have access
- Open access
- Export citation
Intertwined Markov processes: the extended Chapman–Kolmogorov equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 123-131
- Print publication:
- February 2018
-
- Article
- Export citation
On the outcome of epidemics with detections
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 890-904
- Print publication:
- September 2017
-
- Article
- Export citation
Limit theorems for pure death processes coming down from infinity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 720-731
- Print publication:
- September 2017
-
- Article
- Export citation
Simulation from quasi-stationary distributions on reducible state spaces
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 960-980
- Print publication:
- September 2017
-
- Article
- Export citation
Limit theorems for the zig-zag process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 791-825
- Print publication:
- September 2017
-
- Article
- Export citation
The quasispecies regime for the simple genetic algorithm with roulette wheel selection
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 903-926
- Print publication:
- September 2017
-
- Article
- Export citation
Large deviation principle for epidemic models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 905-920
- Print publication:
- September 2017
-
- Article
- Export citation
Weak limits for the largest subpopulations in Yule processes with high mutation probabilities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 877-902
- Print publication:
- September 2017
-
- Article
- Export citation
Computing absorbing times via fluid approximations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 768-790
- Print publication:
- September 2017
-
- Article
- Export citation
On the threshold strategies in optimal stopping problems for diffusion processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 963-969
- Print publication:
- September 2017
-
- Article
- Export citation
ON THE REGULARITY OF SLE TRACE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 24 August 2017, e19
-
- Article
-
- You have access
- Open access
- Export citation