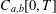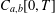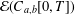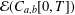Refine listing
Actions for selected content:
1723 results in 60Jxx
A unified approach for large queue asymptotics in a heterogeneous multiserver queue
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 17 March 2017, pp. 182-220
- Print publication:
- March 2017
-
- Article
- Export citation
Subgeometric rates of convergence for Markov processes under subordination
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 17 March 2017, pp. 162-181
- Print publication:
- March 2017
-
- Article
- Export citation
Genealogies of two linked neutral loci after a selective sweep in a large population of stochastically varying size
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 17 March 2017, pp. 279-326
- Print publication:
- March 2017
-
- Article
- Export citation
On occupation times of the first and third quadrants for planar Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 337-342
- Print publication:
- March 2017
-
- Article
- Export citation
Corrected discrete approximations for the conditional and unconditional distributions of the continuous scan statistic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 304-319
- Print publication:
- March 2017
-
- Article
- Export citation
Epidemic risk and insurance coverage
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 286-303
- Print publication:
- March 2017
-
- Article
-
- You have access
- Export citation
Unifying the Dynkin and Lebesgue–Stieltjes formulae
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 252-266
- Print publication:
- March 2017
-
- Article
- Export citation
A REPRESENTATION FOR THE INVERSE GENERALISED FOURIER–FEYNMAN TRANSFORM VIA CONVOLUTION PRODUCT ON FUNCTION SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 05 January 2017, pp. 424-435
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Asymptotic frequency of shapes in supercritical branching trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1143-1155
- Print publication:
- December 2016
-
- Article
- Export citation
Distributions of jumps in a continuous-state branching process with immigration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1166-1177
- Print publication:
- December 2016
-
- Article
- Export citation
Steady-state analysis of a multiclass MAP/PH/c queue with acyclic PH retrials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1098-1110
- Print publication:
- December 2016
-
- Article
- Export citation
The deterministic Kermack‒McKendrick model bounds the general stochastic epidemic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1031-1040
- Print publication:
- December 2016
-
- Article
- Export citation
Speed of coming down from infinity for birth-and-death processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 11 January 2017, pp. 1183-1210
- Print publication:
- December 2016
-
- Article
- Export citation
Branching processes in generalized autoregressive conditional environments
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 11 January 2017, pp. 1211-1234
- Print publication:
- December 2016
-
- Article
- Export citation
Criterion for unlimited growth of critical multidimensional stochastic models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 11 January 2017, pp. 972-988
- Print publication:
- December 2016
-
- Article
- Export citation
On a coalescence process and its branching genealogy
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1156-1165
- Print publication:
- December 2016
-
- Article
- Export citation
Comparison of time-inhomogeneous Markov processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 11 January 2017, pp. 1015-1044
- Print publication:
- December 2016
-
- Article
- Export citation
A stochastic two-stage innovation diffusion model on a lattice
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1019-1030
- Print publication:
- December 2016
-
- Article
- Export citation
On the emergence of random initial conditions in fluid limits
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1193-1205
- Print publication:
- December 2016
-
- Article
- Export citation
A central limit theorem and a law of the iterated logarithm for the Biggins martingale of the supercritical branching random walk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1178-1192
- Print publication:
- December 2016
-
- Article
- Export citation