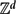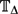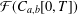Refine listing
Actions for selected content:
1723 results in 60Jxx
Distribution of the quasispecies for a Galton–Watson process on the sharp peak landscape
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 606-613
- Print publication:
- June 2016
-
- Article
- Export citation
Population viewpoint on Hawkes processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 463-480
- Print publication:
- June 2016
-
- Article
- Export citation
EXACT ANALYTICAL EXPRESSIONS FOR THE FINAL EPIDEMIC SIZE OF AN SIR MODEL ON SMALL NETWORKS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 57 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 23 May 2016, pp. 429-444
-
- Article
-
- You have access
- Export citation
Bruckner–Garg-Type Results with Respect to Haar Null Sets in C[0, 1]
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 10 May 2016, pp. 17-30
-
- Article
- Export citation
A Convexity Property of Discrete Random Walks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 31 March 2016, pp. 928-940
-
- Article
- Export citation
The speed of a random walk excited by its recent history
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 215-234
- Print publication:
- March 2016
-
- Article
- Export citation
Correlation formulas for Markovian network processes in a random environment
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 176-198
- Print publication:
- March 2016
-
- Article
- Export citation
Perturbation analysis of inhomogeneous finite Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 255-273
- Print publication:
- March 2016
-
- Article
- Export citation
Optimal learning with non-Gaussian rewards
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 112-136
- Print publication:
- March 2016
-
- Article
- Export citation
Duality and complete convergence for multi-type additive growth models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 32-51
- Print publication:
- March 2016
-
- Article
- Export citation
Inapproximability of the Partition Function for the Antiferromagnetic Ising and Hard-Core Models
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 500-559
-
- Article
- Export citation
Escape from the boundary in Markov population processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 1190-1211
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
The extinction time of a subcritical branching process related to the SIR epidemic on a random graph
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1195-1201
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
The M/M/c queue with mass exodus and mass arrivals when empty
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 990-1002
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Finite-horizon optimality for continuous-time Markov decision processes with unbounded transition rates
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 1064-1087
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Perfect simulation of M/G/c queues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 1039-1063
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Countable state Markov decision processes with unbounded jump rates and discounted cost: optimality equation and approximations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 1088-1107
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
MODEL SELECTION AND ESTIMATING DEGREES OF FREEDOM IN BAYESIAN LINEAR AND LINEAR MIXED EFFECT MODELS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 13 November 2015, pp. 164-166
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
A TRANSLATION THEOREM FOR THE GENERALISED ANALYTIC FEYNMAN INTEGRAL ASSOCIATED WITH GAUSSIAN PATHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 09 September 2015, pp. 152-161
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
First exit time of a Lévy flight from a bounded region in ℝN
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 649-664
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
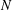
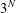
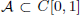 is
is 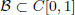 and a Borel probability measure
and a Borel probability measure 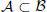 and
and 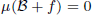 for all
for all