The goal of this paper is to identify exponential convergence rates and to find computable bounds for them for Markov processes representing unreliable Jackson networks. First, we use the bounds of Lawler and Sokal (1988) in order to show that, for unreliable Jackson networks, the spectral gap is strictly positive if and only if the spectral gaps for the corresponding coordinate birth and death processes are positive. Next, utilizing some results on birth and death processes, we find bounds on the spectral gap for network processes in terms of the hazard and equilibrium functions of the one-dimensional marginal distributions of the stationary distribution of the network. These distributions must be in this case strongly light-tailed, in the sense that their discrete hazard functions have to be separated from 0. We relate these hazard functions with the corresponding networks' service rate functions using the equilibrium rates of the stationary one-dimensional marginal distributions. We compare the obtained bounds on the spectral gap with some other known bounds.

In this paper we use the Siegert formula to derive alternative expressions for the moments of the first passage time of the Ornstein-Uhlenbeck process through a constant threshold. The expression for the nth moment is recursively linked to the lower-order moments and consists of only n terms. These compact expressions can substantially facilitate (numerical) applications also for higher-order moments.

In this paper we consider a class of stochastic processes based on binomial observations of continuous-time, Markovian population models. We derive the conditional probability mass function of the next binomial observation given a set of binomial observations. For this purpose, we first find the conditional probability mass function of the underlying continuous-time Markovian population model, given a set of binomial observations, by exploiting a conditional Bayes' theorem from filtering, and then use the law of total probability to find the former. This result paves the way for further study of the stochastic process introduced by the binomial observations. We utilize our results to show that binomial observations of the simple birth process are non-Markovian.

Branching processes are classical growth models in cell kinetics. In their construction, it is usually assumed that cell lifetimes are independent random variables, which has been proved false in experiments. Models of dependent lifetimes are considered here, in particular bifurcating Markov chains. Under the hypotheses of stationarity and multiplicative ergodicity, the corresponding branching process is proved to have the same type of asymptotics as its classic counterpart in the independent and identically distributed supercritical case: the cell population grows exponentially, the growth rate being related to the exponent of multiplicative ergodicity, in a similar way as to the Laplace transform of lifetimes in the i.i.d. case. An identifiable model for which the multiplicative ergodicity coefficients and the growth rate can be explicitly computed is proposed.

In this paper we study a generalized coupon collector problem, which consists of determining the distribution and the moments of the time needed to collect a given number of distinct coupons that are drawn from a set of coupons with an arbitrary probability distribution. We suppose that a special coupon called the null coupon can be drawn but never belongs to any collection. In this context, we obtain expressions for the distribution and the moments of this time. We also prove that the almost-uniform distribution, for which all the nonnull coupons have the same drawing probability, is the distribution which minimizes the expected time to obtain a fixed subset of distinct coupons. This optimization result is extended to the complementary distribution of the time needed to obtain the full collection, proving by the way this well-known conjecture. Finally, we propose a new conjecture which expresses the fact that the almost-uniform distribution should minimize the complementary distribution of the time needed to obtain any fixed number of distinct coupons.

We consider a dynamic metapopulation involving one large population of size N surrounded by colonies of size εN N, usually called peripheral isolates in ecology, where N → ∞ and εN → 0 in such a way that εN N → ∞. The main population, as well as the colonies, independently send propagules to found new colonies (emigration), and each colony independently, eventually merges with the main population (fusion). Our aim is to study the genealogical history of a finite number of lineages sampled at stationarity in such a metapopulation. We make assumptions on model parameters ensuring that the total outer population has size of the order of N and that each colony has a lifetime of the same order. We prove that under these assumptions, the scaling limit of the genealogical process of a finite sample is a censored coalescent where each lineage can be in one of two states: an inner lineage (belonging to the main population) or an outer lineage (belonging to some peripheral isolate). Lineages change state at constant rate and (only) inner lineages coalesce at constant rate per pair. This two-state censored coalescent is also shown to converge weakly, as the landscape dynamics accelerate, to a time-changed Kingman coalescent.

Skeletons of branching processes are defined as trees of lineages characterized by an appropriate signature of future reproduction success. In the supercritical case a natural choice is to look for the lineages that survive forever (O'Connell (1993)). In the critical case it was suggested that the particles with the total number of descendants exceeding a certain threshold could be distinguished (see Sagitov (1997)). These two definitions lead to asymptotic representations of the skeletons as either pure birth process (in the slightly supercritical case) or critical birth-death processes (in the critical case conditioned on the total number of particles exceeding a high threshold value). The limit skeletons reveal typical survival scenarios for the underlying branching processes. In this paper we consider near-critical Bienaymé-Galton-Watson processes and define their skeletons using marking of particles. If marking is rare, such skeletons are approximated by birth and death processes, which can be subcritical, critical, or supercritical. We obtain the limit skeleton for a sequential mutation model (Sagitov and Serra (2009)) and compute the density distribution function for the time to escape from extinction.

This paper concerns discrete-time Markov decision chains with denumerable state and compact action sets. Besides standard continuity requirements, the main assumption on the model is that it admits a Lyapunov function ℓ. In this context the average reward criterion is analyzed from the sample-path point of view. The main conclusion is that if the expected average reward associated to ℓ2 is finite under any policy then a stationary policy obtained from the optimality equation in the standard way is sample-path average optimal in a strong sense.

In this paper we construct some Feller semigroups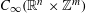, hence Feller processes, with state space $\mathbb{R}^{n}\times \mathbb{Z}^{m}$ starting with pseudo-differential operators having symbols defined on $\mathbb{R}^{n}\times \mathbb{R}^{n}\times \mathbb{Z}^{m}\times \mathbb{T}^{m}$.

In [1], the authors consider a random walk (Z n,1, . . ., Z n,K+1) ∈ ${\mathbb{Z}}$ K+1 with the constraint that each coordinate of the walk is at distance one from the following coordinate. A functional central limit theorem for the first coordinate is proved and the limit variance is explicited. In this paper, we study an extended version of this model by conditioning the extremal coordinates to be at some fixed distance at every time. We prove a functional central limit theorem for this random walk. Using combinatorial tools, we give a precise formula of the variance and compare it with that obtained in [1].

The drawdown process of a one-dimensional regular diffusion process X is given by X reflected at its running maximum. The drawup process is given by X reflected at its running minimum. We calculate the probability that a drawdown precedes a drawup in an exponential time-horizon. We then study the law of the occupation times of the drawdown process and the drawup process. These results are applied to address problems in risk analysis and for option pricing of the drawdown process. Finally, we present examples of Brownian motion with drift and three-dimensional Bessel processes, where we prove an identity in law.

In this paper three models are considered. They are the infinitely-many-neutral-alleles model of Ethier and Kurtz (1981), the two-parameter infinitely-many-alleles diffusion model of Petrov (2009), and the infinitely-many-alleles model with symmetric dominance Ethier and Kurtz (1998). New representations of the transition densities are obtained for the first two models and the ergodic inequalities are provided for all three models.

For a Markov two-dimensional death-process of a special class we consider the use of Fourier methods to obtain an exact solution of the Kolmogorov equations for the exponential (double) generating function of the transition probabilities. Using special functions, we obtain an integral representation for the generating function of the transition probabilities. We state the expression of the expectation and variance of the stochastic process and establish a limit theorem.

In this paper we study the augmented truncation of discrete-time block-monotone Markov chains under geometric drift conditions. We first present a bound for the total variation distance between the stationary distributions of an original Markov chain and its augmented truncation. We also obtain such error bounds for more general cases, where an original Markov chain itself is not necessarily block monotone but is blockwise dominated by a block-monotone Markov chain. Finally, we discuss the application of our results to GI/G/1-type Markov chains.

In this paper, we continue the work started by Steve Krone on the two-stage contact process. We give a simplified proof of the duality relation and answer most of the open questions posed in Krone (1999). We also fill in the details of an incomplete proof.

In this paper our objective is to study continuous-time Markov decision processes on a general Borel state space with both impulsive and continuous controls for the infinite time horizon discounted cost. The continuous-time controlled process is shown to be nonexplosive under appropriate hypotheses. The so-called Bellman equation associated to this control problem is studied. Sufficient conditions ensuring the existence and the uniqueness of a bounded measurable solution to this optimality equation are provided. Moreover, it is shown that the value function of the optimization problem under consideration satisfies this optimality equation. Sufficient conditions are also presented to ensure on the one hand the existence of an optimal control strategy, and on the other hand the existence of a ε-optimal control strategy. The decomposition of the state space into two disjoint subsets is exhibited where, roughly speaking, one should apply a gradual action or an impulsive action correspondingly to obtain an optimal or ε-optimal strategy. An interesting consequence of our previous results is as follows: the set of strategies that allow interventions at time t = 0 and only immediately after natural jumps is a sufficient set for the control problem under consideration.

In this paper we propose the asymptotic error distributions of the Euler scheme for a stochastic differential equation driven by Itô semimartingales. Jacod (2004) studied this problem for stochastic differential equations driven by pure jump Lévy processes and obtained quite sharp results. We extend his results to a more general pure jump Itô semimartingale.

This paper demonstrates the occurrence of the feature called BRAVO (balancing reduces asymptotic variance of output) for the departure process of a finite-buffer Markovian many-server system in the QED (quality and efficiency-driven) heavy-traffic regime. The results are based on evaluating the limit of an equation for the asymptotic variance of death counts in finite birth-death processes.

We study the asymptotics of a Markovian system of N ≥ 3 particles in [0, 1]d in which, at each step in discrete time, the particle farthest from the current centre of mass is removed and replaced by an independent U[0, 1]d random particle. We show that the limiting configuration contains N − 1 coincident particles at a random location ξN ∈ [0, 1]d . A key tool in the analysis is a Lyapunov function based on the squared radius of gyration (sum of squared distances) of the points. For d = 1, we give additional results on the distribution of the limit ξN , showing, among other things, that it gives positive probability to any nonempty interval subset of [0, 1], and giving a reasonably explicit description in the smallest nontrivial case, N = 3.

In this paper we study the speed of infection spread and the survival of the contact process in the random geometric graph G = G(n, r n , f) of n nodes independently distributed in S = [-½, ½]2 according to a certain density f(·). In the first part of the paper we assume that infection spreads from one node to another at unit rate and that infected nodes stay in the same state forever. We provide an explicit lower bound on the speed of infection spread and prove that infection spreads in G with speed at least D 1 nr n 2. In the second part of the paper we consider the contact process ξt on G where infection spreads at rate λ > 0 from one node to another and each node independently recovers at unit rate. 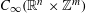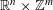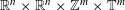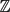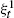We prove that, for every λ > 0, with high probability, the contact process on G survives for an exponentially long time; there exist positive constants c 1 and c 2 such that, with probability at least 1 - c 1 / n 4, the contact process starting with all nodes infected survives up to time t n = exp(c 2 n/logn) for all n.