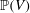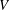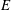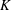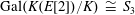Refine listing
Actions for selected content:
1705 results in 60Jxx
Random walks on projective spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 9 / September 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1579-1606
- Print publication:
- September 2014
-
- Article
- Export citation
A Markov model for Selmer ranks in families of twists
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 30 June 2014, pp. 1077-1106
- Print publication:
- July 2014
-
- Article
- Export citation
Convergence of Conditional Metropolis-Hastings Samplers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 422-445
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Parameter Dependent Optimal Thresholds, Indifference Levels and Inverse Optimal Stopping Problems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 492-511
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
On the Asymmetric Telegraph Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 569-589
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
On Asymptotics of the Beta Coalescents
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 496-515
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Convergence and Monotonicity for a Model of Spontaneous Infection and Transmission
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 560-584
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Strong Local Survival of Branching Random Walks is Not Monotone
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 400-421
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Markov Chain Monte Carlo for Computing Rare-Event Probabilities for a Heavy-Tailed Random Walk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 359-376
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Dirichlet and Quasi-Bernoulli Laws for Perpetuities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 400-416
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
The Limiting Behaviour of Hanski's Incidence Function Metapopulation Model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 297-316
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Exact Simulation for Diffusion Bridges: An Adaptive Approach
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 346-358
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Limit Theorems for Continuous-Time Branching Flows
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 317-332
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Stochastic Modeling of Density-Dependent Diploid Populations and the Extinction Vortex
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 446-477
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
A Characterisation of Transient Random Walks on Stochastic Matrices with Dirichlet Distributed Limits
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 542-555
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
On Optimal Retirement
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 333-345
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
ON DISCRETE STOCHASTIC PROCESSES WITH DISJUNCTIVE OUTCOMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 12 May 2014, pp. 149-159
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Joint Densities of First Hitting Times of a Diffusion Process Through Two Time-Dependent Boundaries
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 186-202
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
Species Dynamics in the Two-Parameter Poisson-Dirichlet Diffusion Model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 174-190
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
Bounded Variation Control of Itô Diffusions with Exogenously Restricted Intervention Times
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 102-120
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation