Refine listing
Actions for selected content:
1705 results in 60Jxx
Stochastic Monotonicity and Duality of kth Order with Application to Put-Call Symmetry of Powered Options
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 82-101
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
A Queueing Loss Model with Heterogeneous Skill Based Servers Under Idle Time Ordering Policies
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 269-277
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Eigentime Identity for One-Dimensional Diffusion Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 224-237
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Representations for the Decay Parameter of a Birth-Death Process Based on the Courant-Fischer Theorem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 278-289
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
On the Frequency of Drawdowns for Brownian Motion Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 191-208
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Λ-coalescents: a survey
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 23-40
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Couplings for locally branching epidemic processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 43-56
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Probability Distribution Function for the Euclidean Distance Between Two Telegraph Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 1172-1193
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Quasistochastic matrices and Markov renewal theory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 359-376
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Potential Measures of One-Sided Markov Additive Processes with Reflecting and Terminating Barriers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1154-1170
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Total internal and external lengths of the Bolthausen-Sznitman coalescent
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 73-86
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Lumpings of Markov Chains, Entropy Rate Preservation, and Higher-Order Lumpability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1114-1132
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
On Large Deviations for Small Noise Itô Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 1126-1147
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Spectral Analysis of Markov Kernels and Application to the Convergence Rate Of Discrete Random Walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 1036-1058
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
How did we get here?
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 63-72
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Weak Convergence Rates of Population Versus Single-Chain Stochastic Approximation MCMC Algorithms
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 1059-1083
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Exact estimation for Markov chain equilibrium expectations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 377-389
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Type Transition of Simple Random Walks on Randomly Directed Regular Lattices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1065-1080
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Approximations: replacing random variables with their means
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 57-62
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Markov Tail Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1133-1153
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
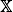 with transition kernel
with transition kernel 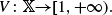 The Markov kernel
The Markov kernel 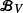 associated with
associated with 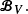 A general procedure to compute ρ
A general procedure to compute ρ