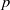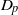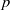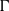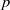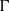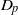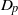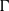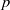Refine listing
Actions for selected content:
1705 results in 60Jxx
Stochastic Sequences with a Regenerative Structure that May Depend Both on the Future and on the Past
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 1083-1110
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Extinction Probabilities of Branching Processes with Countably Infinitely Many Types
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 1068-1082
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Acquaintance Vaccination in an Epidemic on a Random Graph with Specified Degree Distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1147-1168
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Discrete, Continuous and Conditional Multiple Window Scan Statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1089-1101
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Markov Processes with Restart
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 960-968
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
A Host-Parasite Model for a Two-Type Cell Population
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 719-741
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
Stochastic Models for a Chemostat and Long-Time Behavior
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 822-836
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
Hitting Times, Occupation Times, Trivariate Laws and the Forward Kolmogorov Equation for a One-Dimensional Diffusion with Memory
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 860-875
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
Discrete-Time Approximation of Decoupled Forward‒Backward Stochastic Differential Equations Driven by Pure Jump Lévy Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 791-821
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
On Largest Offspring in a Critical Branching Process with Finite Variance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 791-800
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
A Construction of a β-Coalescent via the Pruning of Binary Trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 772-790
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
The Expected Total Cost Criterion for Markov Decision Processes under Constraints
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 837-859
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
An Application of the Coalescence Theory to Branching Random Walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 893-899
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
THE
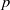 $p$-HARMONIC BOUNDARY AND
$p$-HARMONIC BOUNDARY AND 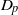 ${D}_{p} $-MASSIVE SUBSETS OF A GRAPH OF BOUNDED DEGREE
${D}_{p} $-MASSIVE SUBSETS OF A GRAPH OF BOUNDED DEGREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 12 June 2013, pp. 149-158
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
Stability of the Bipartite Matching Model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 22 February 2016, pp. 351-378
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Coalescence in Subcritical Bellman-Harris Age-Dependent Branching Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 576-591
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Absorbing Continuous-Time Markov Decision Processes with Total Cost Criteria
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 22 February 2016, pp. 490-519
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Pruned Discrete Random Samples
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 542-556
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Generalized Telegraph Process with Random Jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 450-463
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
A Markov Additive Risk Process with a Dividend Barrier
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 22 February 2016, pp. 451-489
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation