Refine listing
Actions for selected content:
1705 results in 60Jxx
Nonlinear Filtering for Jump Diffusion Observations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 678-701
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Fractional Brownian Motion with H < 1/2 as a Limit of Scheduled Traffic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 710-718
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Exit Problems for Reflected Markov-Modulated Brownian Motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 697-709
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Coalescence in Critical and Subcritical Galton-Watson Branching Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 627-638
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Option Pricing Driven by a Telegraph Process with Random Jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 838-849
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Backward Coalescence Times for Perfect Simulation of Chains with Infinite Memory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 319-337
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
On Optimal Stopping Problems for Matrix-Exponential Jump-Diffusion Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 531-548
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Means and Variances in Stochastic Multistage Cancer Models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 590-594
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Hurst Index of Functions of Long-Range-Dependent Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 451-471
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
A Central Limit Theorem for a Discrete-Time SIS Model with Individual Variation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 521-530
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
On Rice's Formula for Stationary Multivariate Piecewise Smooth Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 351-363
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Lie Algebra Solution of Population Models Based on Time-Inhomogeneous Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 472-481
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
A Symmetry Property for a Class of Random Walks in Stationary Random Environments on Z
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 338-350
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Implicit Renewal Theory and Power Tails on Trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 528-561
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Stein's Method and Stochastic Orderings
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 343-372
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Occupation Times for Markov-Modulated Brownian Motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 549-565
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
A Self-Normalized Central Limit Theorem for Markov Random Walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 452-478
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
ASYMPTOTIC BEHAVIOUR OF RANDOM MARKOV CHAINS WITH TRIDIAGONAL GENERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 30 March 2012, pp. 27-36
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
STABILITY OF SINGULAR JUMP-LINEAR SYSTEMS WITH A LARGE STATE SPACE: A TWO-TIME-SCALE APPROACH
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 4 / April 2011
- Published online by Cambridge University Press:
- 20 March 2012, pp. 372-390
-
- Article
-
- You have access
- Export citation
The Smooth-Fit Property in an Exponential Lévy Model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 137-149
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
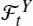 provides all the available information about
provides all the available information about 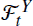 . To this end, we prove that π
. To this end, we prove that π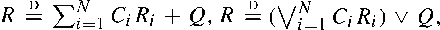 and similar recursions, where (
and similar recursions, where (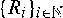 are independent and identically distributed copies of
are independent and identically distributed copies of  , and is adjoined to the chain such that {
, and is adjoined to the chain such that {