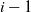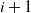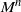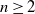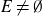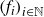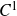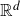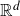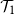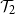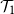Refine listing
Actions for selected content:
1723 results in 60Jxx
Non-Gaussian fluctuations of randomly trapped random walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 801-838
- Print publication:
- September 2021
-
- Article
- Export citation
Subgeometric ergodicity and β-mixing
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 594-608
- Print publication:
- September 2021
-
- Article
- Export citation
Variational inference for Markovian queueing networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 687-715
- Print publication:
- September 2021
-
- Article
-
- You have access
- HTML
- Export citation
Avalanches in a short-memory excitable network
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 609-648
- Print publication:
- September 2021
-
- Article
- Export citation
Diffusion approximation of multi-class Hawkes processes: Theoretical and numerical analysis
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 716-756
- Print publication:
- September 2021
-
- Article
- Export citation
Stochastic ordering for birth–death processes with killing
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 708-720
- Print publication:
- September 2021
-
- Article
- Export citation
Detailed balance, local detailed balance, and global potential for stochastic chemical reaction networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 886-922
- Print publication:
- September 2021
-
- Article
- Export citation
Variations of the elephant random walk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 805-829
- Print publication:
- September 2021
-
- Article
- Export citation
Controlled branching processes with continuous time
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 830-848
- Print publication:
- September 2021
-
- Article
- Export citation
The distance profile of rooted and unrooted simply generated trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 18 August 2021, pp. 368-410
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classification of backward filtrations and factor filtrations: examples from cellular automata
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 21 July 2021, pp. 2890-2922
- Print publication:
- September 2022
-
- Article
- Export citation
Mixing rates for potentials of non-summable variations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 16 July 2021, pp. 2823-2840
- Print publication:
- September 2022
-
- Article
- Export citation
Random fractals and their intersection with winning sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 07 July 2021, pp. 655-684
- Print publication:
- May 2022
-
- Article
- Export citation
Continuous phase transitions on Galton–Watson trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 198-228
-
- Article
- Export citation
Optimal transportation and stationary measures for iterated function systems
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 28 June 2021, pp. 163-187
- Print publication:
- July 2022
-
- Article
- Export citation
Risk-sensitive average continuous-time Markov decision processes with unbounded transition and cost rates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 523-550
- Print publication:
- June 2021
-
- Article
- Export citation
On gradual-impulse control of continuous-time Markov decision processes with exponential utility
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 July 2021, pp. 301-334
- Print publication:
- June 2021
-
- Article
- Export citation
A product form for the general stochastic matching model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 449-468
- Print publication:
- June 2021
-
- Article
- Export citation
Ruin problems for epidemic insurance
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 July 2021, pp. 484-509
- Print publication:
- June 2021
-
- Article
- Export citation
Population dynamics driven by truncated stable processes with Markovian switching
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 505-522
- Print publication:
- June 2021
-
- Article
- Export citation