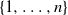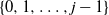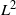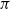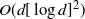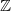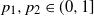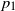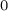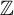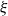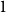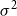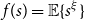Refine listing
Actions for selected content:
1723 results in 60Jxx
A probabilistic model for interfaces in a martensitic phase transition
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 09 August 2022, pp. 1081-1105
- Print publication:
- December 2022
-
- Article
-
- You have access
- HTML
- Export citation
A unifying approach to non-minimal quasi-stationary distributions for one-dimensional diffusions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 08 August 2022, pp. 1106-1128
- Print publication:
- December 2022
-
- Article
- Export citation
Scaling limits of branching random walks and branching-stable processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 04 August 2022, pp. 1009-1025
- Print publication:
- December 2022
-
- Article
- Export citation
A new matrix-infinite-product-form solution for upper block-Hessenberg Markov chains and its quasi-algorithmic constructibility
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 29 July 2022, pp. 1-28
- Print publication:
- March 2023
-
- Article
- Export citation
A note on the polynomial ergodicity of the one-dimensional Zig-Zag process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 18 July 2022, pp. 895-903
- Print publication:
- September 2022
-
- Article
- Export citation
The hit-and-run version of top-to-random
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 12 July 2022, pp. 860-879
- Print publication:
- September 2022
-
- Article
- Export citation
Skew brownian motion and complexity of the alps algorithm
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 12 July 2022, pp. 777-796
- Print publication:
- September 2022
-
- Article
- Export citation
Mutually interacting superprocesses with migration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 July 2022, pp. 904-929
- Print publication:
- September 2022
-
- Article
- Export citation
On supercritical branching processes with emigration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 08 July 2022, pp. 734-754
- Print publication:
- September 2022
-
- Article
- Export citation
Hitting times for second-order random walks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 04 July 2022, pp. 642-666
-
- Article
- Export citation
Coexistence of lazy frogs on
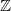 ${\mathbb{Z}}$
${\mathbb{Z}}$
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 28 June 2022, pp. 702-713
- Print publication:
- September 2022
-
- Article
- Export citation
Discounted optimal stopping problems in first-passage time models with random thresholds
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 27 June 2022, pp. 714-733
- Print publication:
- September 2022
-
- Article
- Export citation
Unbiased filtering of a class of partially observed diffusions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 661-687
- Print publication:
- September 2022
-
- Article
- Export citation
Spectral analysis of bilateral birth–death processes: some new explicit examples
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 1193-1221
- Print publication:
- December 2022
-
- Article
- Export citation
Gradient estimation for smooth stopping criteria
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 15 June 2022, pp. 29-55
- Print publication:
- March 2023
-
- Article
- Export citation
Central limit theorem for bifurcating markov chains under L2-ergodic conditions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 999-1031
- Print publication:
- December 2022
-
- Article
- Export citation
Moments of Markovian growth–collapse processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1070-1093
- Print publication:
- December 2022
-
- Article
- Export citation
BERNOULLI ACTIONS OF TYPE III
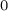 $_0$ WITH PRESCRIBED ASSOCIATED FLOW
$_0$ WITH PRESCRIBED ASSOCIATED FLOW
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 14 June 2022, pp. 71-122
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probability of total domination for transient reflecting processes in a quadrant
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1094-1138
- Print publication:
- December 2022
-
- Article
- Export citation
On the peel number and the leaf-height of Galton–Watson trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 09 June 2022, pp. 68-90
-
- Article
- Export citation