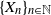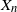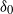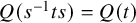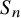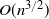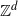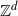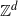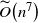Refine listing
Actions for selected content:
1723 results in 60Jxx
On the probability of rumour survival among sceptics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 02 March 2023, pp. 1096-1111
- Print publication:
- September 2023
-
- Article
- Export citation
Robustness of iterated function systems of Lipschitz maps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 28 February 2023, pp. 921-944
- Print publication:
- September 2023
-
- Article
- Export citation
Multiple random walks on graphs: mixing few to cover many
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 15 February 2023, pp. 594-637
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A dual risk model with additive and proportional gains: ruin probability and dividends
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 08 February 2023, pp. 549-580
- Print publication:
- June 2023
-
- Article
- Export citation
Reciprocal properties of random fields on undirected graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 781-796
- Print publication:
- September 2023
-
- Article
- Export citation
Sturm–Liouville theory and decay parameter for quadratic markov branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 January 2023, pp. 737-764
- Print publication:
- September 2023
-
- Article
- Export citation
Critical branching as a pure death process coming down from infinity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 January 2023, pp. 607-628
- Print publication:
- June 2023
-
- Article
- Export citation
Transition density of an infinite-dimensional diffusion with the jack parameter
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 16 January 2023, pp. 797-811
- Print publication:
- September 2023
-
- Article
- Export citation
Invariant Galton–Watson trees: metric properties and attraction with respect to generalized dynamical pruning
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 643-671
- Print publication:
- June 2023
-
- Article
- Export citation
Convergence of blanket times for sequences of random walks on critical random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 09 January 2023, pp. 478-515
-
- Article
- Export citation
Double coset Markov chains
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 January 2023, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis of a non-reversible Markov chain speedup by a single edge
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 04 January 2023, pp. 642-660
- Print publication:
- June 2023
-
- Article
- Export citation
Local limit theorem for a Markov additive process on
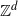 $\mathbb{Z}^d$ with a null recurrent internal Markov chain
$\mathbb{Z}^d$ with a null recurrent internal Markov chain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 22 December 2022, pp. 570-588
- Print publication:
- June 2023
-
- Article
- Export citation
Exponential ergodicity for a class of Markov processes with interactions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 01 December 2022, pp. 465-478
- Print publication:
- June 2023
-
- Article
- Export citation
On random walks and switched random walks on homogeneous spaces
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 28 November 2022, pp. 398-421
-
- Article
- Export citation
The fundamental inequality for cocompact Fuchsian groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 November 2022, e102
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ruin probabilities in a Markovian shot-noise environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 11 November 2022, pp. 542-556
- Print publication:
- June 2023
-
- Article
- Export citation
Strong couplings for static locally tree-like random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 11 November 2022, pp. 1261-1285
- Print publication:
- December 2022
-
- Article
- Export citation
John’s walk
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 10 November 2022, pp. 473-491
- Print publication:
- June 2023
-
- Article
- Export citation
Branching Brownian motion in a periodic environment and uniqueness of pulsating traveling waves
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 09 November 2022, pp. 510-548
- Print publication:
- June 2023
-
- Article
- Export citation