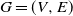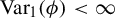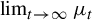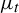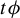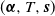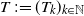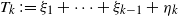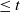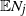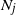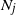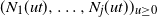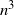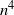Refine listing
Actions for selected content:
1723 results in 60Jxx
A growth-fragmentation model connected to the ricocheted stable process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 08 November 2022, pp. 493-503
- Print publication:
- June 2023
-
- Article
- Export citation
On decay–surge population models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 08 November 2022, pp. 444-472
- Print publication:
- June 2023
-
- Article
- Export citation
Brownian bridge expansions for Lévy area approximations and particular values of the Riemann zeta function
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 03 November 2022, pp. 370-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A transport process on graphs and its limiting distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 October 2022, pp. 341-357
- Print publication:
- March 2023
-
- Article
- Export citation
Anomalous recurrence of Markov chains on negatively curved manifolds
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 204-222
- Print publication:
- March 2023
-
- Article
- Export citation
Existence of the zero-temperature limit of equilibrium states on topologically transitive countable Markov shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 3231-3254
- Print publication:
- October 2023
-
- Article
- Export citation
A Markov jump process associated with the matrix-exponential distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 20 September 2022, pp. 1-13
- Print publication:
- March 2023
-
- Article
- Export citation
From reflected Lévy processes to stochastically monotone Markov processes via generalized inverses and supermodularity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 19 September 2022, pp. 68-84
- Print publication:
- March 2023
-
- Article
- Export citation
On the study of the running maximum and minimum level of level-dependent quasi-birth–death processes and related models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 19 September 2022, pp. 14-29
- Print publication:
- March 2023
-
- Article
- Export citation
Critical cluster cascades
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 13 September 2022, pp. 357-381
- Print publication:
- June 2023
-
- Article
- Export citation
Full classification of dynamics for one-dimensional continuous-time Markov chains with polynomial transition rates
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 12 September 2022, pp. 321-355
- Print publication:
- March 2023
-
- Article
- Export citation
Matrix calculations for moments of Markov processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 126-150
- Print publication:
- March 2023
-
- Article
- Export citation
Fast mixing of a randomized shift-register Markov chain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 253-266
- Print publication:
- March 2023
-
- Article
- Export citation
Renewal theory for iterated perturbed random walks on a general branching process tree: Early generations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 45-67
- Print publication:
- March 2023
-
- Article
- Export citation
An adjacent-swap Markov chain on coalescent trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 September 2022, pp. 1243-1260
- Print publication:
- December 2022
-
- Article
- Export citation
On q-scale functions of spectrally negative Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 56-84
- Print publication:
- March 2023
-
- Article
- Export citation
The rescaled Pólya urn: local reinforcement and chi-squared goodness-of-fit test
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 18 October 2022, pp. 849-879
- Print publication:
- September 2022
-
- Article
- Export citation
Surprising identities for the greedy independent set on Cayley trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 25 August 2022, pp. 1042-1058
- Print publication:
- December 2022
-
- Article
- Export citation
Random population dynamics under catastrophic events
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 15 August 2022, pp. 962-982
- Print publication:
- December 2022
-
- Article
- Export citation
Exponential convergence to a quasi-stationary distribution for birth–death processes with an entrance boundary at infinity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 August 2022, pp. 983-991
- Print publication:
- December 2022
-
- Article
- Export citation