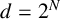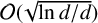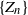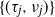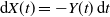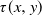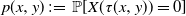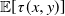Refine listing
Actions for selected content:
1723 results in 60Jxx
Improved Metropolis–Hastings algorithms via landscape modification with applications to simulated annealing and the Curie–Weiss model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 30 August 2023, pp. 587-620
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Adaptation of a population to a changing environment in the light of quasi-stationarity
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 30 August 2023, pp. 235-286
- Print publication:
- March 2024
-
- Article
- Export citation
ON THE EXPECTED UNIFORM ERROR OF BROWNIAN MOTION APPROXIMATED BY THE LÉVY–CIESIELSKI CONSTRUCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 581-593
- Print publication:
- June 2024
-
- Article
- Export citation
Branching processes in random environments with thresholds
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 495-544
- Print publication:
- June 2024
-
- Article
- Export citation
MECHANISTIC MARKOV MODELS FOR THE EVOLUTION OF GENE FAMILIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 10 August 2023, pp. 513-515
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
Heavy-traffic limits for parallel single-server queues with randomly split Hawkes arrival processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 07 August 2023, pp. 490-514
- Print publication:
- June 2024
-
- Article
- Export citation
Chase–escape in dynamic device-to-device networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 07 August 2023, pp. 311-339
- Print publication:
- March 2024
-
- Article
- Export citation
Disparity-persistence and the multistep friendship paradox
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 25 July 2023, pp. 290-298
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sensitivity of mixing times of Cayley graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 18 July 2023, pp. 1400-1431
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PDE for the joint law of the pair of a continuous diffusion and its running maximum
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 10 July 2023, pp. 1171-1210
- Print publication:
- December 2023
-
- Article
- Export citation
An elementary approach to the inverse first-passage-time problem for soft-killed Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 July 2023, pp. 279-300
- Print publication:
- March 2024
-
- Article
- Export citation
Optimal coupling of jumpy Brownian motion on the circle
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 July 2023, pp. 18-32
- Print publication:
- March 2024
-
- Article
- Export citation
OPTIMAL STOPPING PROBLEMS WITH A RANDOM TIME HORIZON
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 29 June 2023, pp. 345-346
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
CONDITIONS FOR RECURRENCE AND TRANSIENCE FOR TIME-INHOMOGENEOUS BIRTH-AND-DEATH PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 393-402
- Print publication:
- April 2024
-
- Article
- Export citation
ESSAYS ON STRONG AND WEAK APPROXIMATIONS OF STOCHASTIC DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 175-176
- Print publication:
- August 2023
-
- Article
-
- You have access
- HTML
- Export citation
Explosion of continuous-state branching processes with competition in a Lévy environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 09 June 2023, pp. 68-81
- Print publication:
- March 2024
-
- Article
- Export citation
Propagation of chaos and large deviations in mean-field models with jumps on block-structured networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 05 June 2023, pp. 1301-1361
- Print publication:
- December 2023
-
- Article
- Export citation
Exact convergence analysis for metropolis–hastings independence samplers in Wasserstein distances
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 33-54
- Print publication:
- March 2024
-
- Article
- Export citation
A branching random walk in the presence of a hard wall
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 22 May 2023, pp. 1-17
- Print publication:
- March 2024
-
- Article
- Export citation
A first-passage-place problem for integrated diffusion processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 22 May 2023, pp. 55-67
- Print publication:
- March 2024
-
- Article
- Export citation