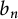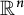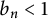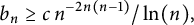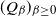Refine listing
Actions for selected content:
1723 results in 60Jxx
On the Kolmogorov constant explicit form in the theory of discrete-time stochastic branching systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 04 January 2024, pp. 927-941
- Print publication:
- September 2024
-
- Article
- Export citation
Weak convergence of the extremes of branching Lévy processes with regularly varying tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 December 2023, pp. 622-643
- Print publication:
- June 2024
-
- Article
- Export citation
Speed of extinction for continuous-state branching processes in a weakly subcritical Lévy environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 886-908
- Print publication:
- September 2024
-
- Article
- Export citation
A subgeometric convergence formula for finite-level M/G/1-type Markov chains: via a block-decomposition-friendly solution to the Poisson equation of the deviation matrix
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 389-429
- Print publication:
- June 2024
-
- Article
- Export citation
Dynamics of information networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 30 November 2023, pp. 1029-1039
- Print publication:
- September 2024
-
- Article
- Export citation
Local convergence of critical Galton–Watson trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 30 November 2023, pp. 851-857
- Print publication:
- September 2024
-
- Article
- Export citation
Tessellation-valued processes that are generated by cell division
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 01 November 2023, pp. 697-715
- Print publication:
- June 2024
-
- Article
- Export citation
Trajectory fitting estimation for reflected stochastic linear differential equations of a large signal
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 31 October 2023, pp. 741-754
- Print publication:
- September 2024
-
- Article
- Export citation
A large-deviation principle for birth–death processes with a linear rate of downward jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 31 October 2023, pp. 781-801
- Print publication:
- September 2024
-
- Article
- Export citation
Differential Harnack estimates for a weighted nonlinear parabolic equation under a super Perelman–Ricci flow and implications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 27 October 2023, pp. 687-717
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lower bounds on Bourgain’s constant for harmonic measure
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1967-1986
- Print publication:
- December 2024
-
- Article
- Export citation
Boolean percolation on digraphs and random exchange processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 25 October 2023, pp. 755-766
- Print publication:
- September 2024
-
- Article
- Export citation
An inaccuracy measure between non-explosive point processes with applications to Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 25 October 2023, pp. 735-756
- Print publication:
- June 2024
-
- Article
- Export citation
Effects of concurrency on epidemic spreading in Markovian temporal networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 18 October 2023, pp. 430-461
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The asymptotic tails of limit distributions of continuous-time Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 693-734
- Print publication:
- June 2024
-
- Article
- Export citation
Collapse and diffusion in harmonic activation and transport
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 September 2023, e85
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the quasi-ergodicity of absorbing Markov chains with unbounded transition densities, including random logistic maps with escape
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 25 September 2023, pp. 1818-1855
- Print publication:
- July 2024
-
- Article
- Export citation
R-positivity and the existence of zero-temperature limits of Gibbs measures on nearest-neighbor matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 25 September 2023, pp. 558-577
- Print publication:
- June 2024
-
- Article
- Export citation
Comparison theorem and stability under perturbation of transition rate matrices for regime-switching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 14 September 2023, pp. 540-557
- Print publication:
- June 2024
-
- Article
- Export citation
Strong convergence of an epidemic model with mixing groups
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 01 September 2023, pp. 430-463
- Print publication:
- June 2024
-
- Article
- Export citation