Refine listing
Actions for selected content:
1446 results in 60Kxx
Near Complete Decomposability: Bounding the Error by a Stochastic Comparison Method
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 830-855
- Print publication:
- September 1997
-
- Article
- Export citation
Regularity and reversibility results for birth-death-migration processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 685-697
- Print publication:
- September 1997
-
- Article
- Export citation
Large deviations for departures from a shared buffer
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 753-766
- Print publication:
- September 1997
-
- Article
- Export citation
Partial balances in batch arrival batch service and assemble-transfer queueing networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 745-752
- Print publication:
- September 1997
-
- Article
- Export citation
Non-Skip-Free M/G/1 and G/M/1 Type Markov Chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 733-758
- Print publication:
- September 1997
-
- Article
- Export citation
A note on stochastic ordering of order statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 785-789
- Print publication:
- September 1997
-
- Article
- Export citation
Extremes for shot noise processes with heavy tailed amplitudes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 643-656
- Print publication:
- September 1997
-
- Article
- Export citation
Corrected Diffusion Approximations for Ruin Probabilities in a Markov Random Walk
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 695-712
- Print publication:
- September 1997
-
- Article
- Export citation
A stationary Poisson departure process from a minimally delayed infinite server queue with non-stationary Poisson arrivals
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 767-772
- Print publication:
- September 1997
-
- Article
- Export citation
On a property of a refusals stream
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 800-805
- Print publication:
- September 1997
-
- Article
- Export citation
Sengupta's invariant relationship and its application to waiting time inference
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 795-799
- Print publication:
- September 1997
-
- Article
- Export citation
Heavy traffic analysis for continuous polling models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 720-732
- Print publication:
- September 1997
-
- Article
- Export citation
Asymptotic Estimates for Blocking Probabilities in a Large Multi-Rate Loss Network
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 806-829
- Print publication:
- September 1997
-
- Article
- Export citation
The geometric convergence rate of a Lindley random walk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 806-811
- Print publication:
- September 1997
-
- Article
- Export citation
An M/G/1 queue with multiple types of feedback and gated vacations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 773-784
- Print publication:
- September 1997
-
- Article
- Export citation
Laplace transforms and the renewal equation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 395-403
- Print publication:
- June 1997
-
- Article
- Export citation
Monotonicity results for MR/GI/1 queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 514-524
- Print publication:
- June 1997
-
- Article
- Export citation
Strong Approximations of Irreducible Closed Queueing Networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 498-522
- Print publication:
- June 1997
-
- Article
- Export citation
Continuity and convergence of the percolation function in continuum percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 363-371
- Print publication:
- June 1997
-
- Article
- Export citation
Strong convergence of proportions in a multicolor Pólya urn
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 426-435
- Print publication:
- June 1997
-
- Article
- Export citation
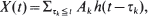 , where {
, where {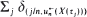 are shown to converge to a compound Poisson point process limit. As a corollary to this result, the joint limiting distribution of high local maxima is obtained.
are shown to converge to a compound Poisson point process limit. As a corollary to this result, the joint limiting distribution of high local maxima is obtained.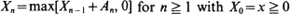 . Here, {
. Here, {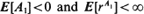 for some
for some 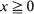 . In this communication we supply a short proof and some extensions of a large deviations result initially due to Veraverbeke and Teugels (1975, 1976): the largest
. In this communication we supply a short proof and some extensions of a large deviations result initially due to Veraverbeke and Teugels (1975, 1976): the largest  and
and 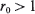 satisfies
satisfies 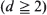 which consists of spheres centred at the points of a Poisson point process of intensity
which consists of spheres centred at the points of a Poisson point process of intensity 