The gating mechanism of a single ion channel is usually modelled by a continuous-time Markov chain with a finite state space. The state space is partitioned into two classes, termed ‘open’ and ‘closed’, and it is possible to observe only which class the process is in. In many experiments channel openings occur in bursts. This can be modelled by partitioning the closed states further into ‘short-lived’ and ‘long-lived’ closed states, and defining a burst of openings to be a succession of open sojourns separated by closed sojourns that are entirely within the short-lived closed states. There is also evidence that bursts of openings are themselves grouped together into clusters. This clustering of bursts can be described by the ratio of the variance Var (N(t)) to the mean [N(t)] of the number of bursts of openings commencing in (0, t]. In this paper two methods of determining Var (N(t))/[N(t)] and limt→∝ Var (N(t))/[N(t)] are developed, the first via an embedded Markov renewal process and the second via an augmented continuous-time Markov chain. The theory is illustrated by a numerical study of a molecular stochastic model of the nicotinic acetylcholine receptor. Extensions to semi-Markov models of ion channel gating and the incorporation of time interval omission are briefly discussed.

We consider the queueing system denoted by M/MN /1/N where customers are served in batches of maximum size N. The model is motivated by a traffic application. The time-dependent probability distribution for the number of customers in the system is obtained in closed form. The solution is used to predict the optimal service rates during a finite time horizon.

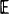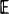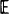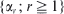An M/M/1 queue is subject to mass exodus at rate β and mass immigration at rate when idle. A general resolvent approach is used to derive occupation probabilities and high-order moments. This powerful technique is not only considerably easier to apply than a standard direct attack on the forward p.g.f. equation, but it also implicitly yields necessary and sufficient conditions for recurrence, positive recurrence and transience.

In this article we define the s-order equilibrium distribution of a life distribution and establish some interesting properties regarding moments for s-order equilibrium distributions. Results are expected to be useful in reliability and renewal processes.

In this paper, we present results for the steady-state system length distributions of the discrete-time GI/G/1 queue. We examine the system at customer arrival epochs (customer departure epochs) and use the residual service time (residual interarrival time) as the supplementary variable. The embedded Markov chain is of GI/M/1 type if the embedding points are arrival epochs and is of M/G/1 type if the embedding points are departure epochs. Using the matrix analytic method, we identify the necessary and sufficient condition for both Markov chains to be positive recurrent. For the GI/M/1 type chain, we derive a matrix-geometric solution for its steady-state distribution and for the M/G/1 type chain, we develop a simple linear transformation that relates it to the GI/M/1 type chain and leads to a simple analytic solution for its steady-state distribution. We also show that the steady-state system length distribution at an arbitrary point in time can be obtained by a simple linear transformation of the matrix-geometric solution for the GI/M/1 type chain. A number of applications of the model to communication systems and numerical examples are also discussed.

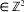In the epidemic with removal with range r, each site z, once infected, remains so for a period of time Tz , the variables Tz being i.i.d. with mean μ. While infected, a site infects its healthy r-neighbours independently at total rate α. After infection, sites become immune. We show that the critical rate of infection αc (r), above which an epidemic starting from a single site may continue forever, converges to μ–1 as r →∞.

A disaster occurs in a queue when a negative arrival causes all the work (and therefore customers) to leave the system instantaneously. Recent papers have addressed several issues pertaining to queueing networks with negative arrivals under the i.i.d. exponential service times assumption. Here we relax this assumption and derive a Pollaczek–Khintchine-like formula for M/G/1 queues with disasters by making use of the preemptive LIFO discipline. As a byproduct, the stationary distribution of the remaining service time process is obtained for queues operating under this discipline. Finally, as an application, we obtain the Laplace transform of the stationary remaining service time of the customer in service for unstable preemptive LIFO M/G/1 queues.

Let P be an infinite irreducible stochastic matrix, recurrent positive and stochastically monotone and Pn be any n × n stochastic matrix with Pn ≧ Tn , where Tn denotes the n × n northwest corner truncation of P. These assumptions imply the existence of limit distributions π and πn for P and Pn respectively. 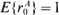We show that if the Markov chain with transition probability matrix P meets the further condition of geometric recurrence then the exact convergence rate of πn to π can be expressed in terms of the radius of convergence of the generating function of π. As an application of the preceding result, we deal with the random walk on a half line and prove that the assumption of geometric recurrence can be relaxed. We also show that if the i.i.d. input sequence (A(m)) is such that we can find a real number r 0 > 1 with , then the exact convergence rate of πn to π is characterized by r 0. Moreover, when the generating function of A is not defined for |z| > 1, we derive an upper bound for the distance between πn and π based on the moments of A.

The time-dependent virtual waiting time in a M/G/1 queue converges to a proper limit when the traffic intensity is less than one. In this paper we give precise rates on the speed of this convergence when the service time distribution has a heavy regularly varying tail.

The result also applies to the classical ruin problem. We obtain the exact rate of convergence for the ruin probability after time t for the case where claims arrive according to a Poisson process and claim sizes are heavy tailed.

Our result supplements similar theorems on exponential convergence rates for relaxation times in queueing theory and ruin probabilities in risk theory.

Based on a semi-Markov process J(t), t ≧ 0, a reward process Z(t), t ≧ 0, is introduced where it is assumed that the reward function, p(k, x) is nonlinear; if the reward function is linear, i.e. ρ (k, x) = kx, the reward process Z(t), t ≧ 0, becomes the classical one, which has been considered by many authors. An explicit formula for E(Z(t)) is given in terms of the moments of the sojourn time distribution at t, when the reward function is a polynomial.

The distribution of the sample quantiles of random processes is important for the pricing of some of the so-called financial ‘look-back' options. In this paper a representation of the distribution of the α-quantile of an additive renewal reward process is obtained as the sum of the supremum and the infimum of two rescaled independent copies of the process. This representation has already been proved for processes with stationary and independent increments. As an example, the distribution of the α-quantile of a randomly observed Brownian motion is obtained.

We establish stability, monotonicity, concavity and subadditivity properties for open stochastic storage networks in which the driving process has stationary increments. A principal example is a stochastic fluid network in which the external inputs are random but all internal flows are deterministic. For the general model, the multi-dimensional content process is tight under the natural stability condition. The multi-dimensional content process is also stochastically increasing when the process starts at the origin, implying convergence to a proper limit under the natural stability condition. In addition, the content process is monotone in its initial conditions. Hence, when any content process with non-zero initial conditions hits the origin, it couples with the content process starting at the origin. However, in general, a tight content process need not hit the origin.

We consider the position of a tagged particle in the one-dimensional asymmetric nearest-neighbor simple exclusion process. Each particle attempts to jump to the site to its right at rate p and to the site to its left at rate q. The jump is realized if the destination site is empty. We assume p > q. The initial distribution is the product measure with density λ, conditioned to have a particle at the origin. We call X, the position at time t of this particle. Using a result recently proved by the authors for a semi-infinite zero-range process, it is shown that for all t ≧ 0, Xt = Nt − Bt + B 0 , where {N t} is a Poisson process of parameter (p – q)(1– λ) and {Bt } is a stationary process satisfying E exp (θ | B, |) < ∞ for some θ > 0. As a corollary we obtain that, properly centered and rescaled, the process {Xt } converges to Brownian motion. A previous result says that in the scale t 1/2, the position Xt is given by the initial number of empty sites in the interval (0, λt) divided by λ. We use this to compute the asymptotic covariance at time t of two tagged particles initially at sites 0 and rt. The results also hold for the net flux between two queues in a system of infinitely many queues in series.

In 1979, Melamed proved that, in an open migration process, the absence of ‘loops' is necessary and sufficient for the equilibrium flow along a link to be a Poisson process. In this paper, we prove approximation theorems with the same flavour: the difference between the equilibrium flow along a link and a Poisson process with the same rate is bounded in terms of expected numbers of loops. The proofs are based on Stein's method, as adapted for bounds on the distance of the distribution of a point process from a Poisson process in Barbour and Brown (1992b). Three different distances are considered, and illustrated with an example consisting of a system of tandem queues with feedback. The upper bound on the total variation distance of the process grows linearly with time, and a lower bound shows that this can be the correct order of approximation.

It is known that a generalized open Jackson queueing network after appropriate scaling (in both time and space) converges almost surely to a fluid network under the uniform topology. Under the same topology, we show that the distance between the scaled queue length process of the queueing network and the fluid level process of the corresponding fluid network converges to zero in probability at an exponential rate.

As a model for an ATM switch we consider the overflow frequency of a queue that is served at a constant rate and in which the arrival process is the superposition of N traffic streams. We consider an asymptotic as N → ∞ in which the service rate Nc and buffer size Nb also increase linearly in N. In this regime, the frequency of buffer overflow is approximately exp(–NI(c, b)), where I(c, b) is given by the solution to an optimization problem posed in terms of time-dependent logarithmic moment generating functions. Experimental results for Gaussian and Markov modulated fluid source models show that this asymptotic provides a better estimate of the frequency of buffer overflow than ones based on large buffer asymptotics.

The so-called ‘Swiss Army formula', derived by Brémaud, seems to be a general purpose relation which includes all known relations of Palm calculus for stationary stochastic systems driven by point processes. The purpose of this article is to present a short, and rather intuitive, proof of the formula. The proof is based on the Ryll–Nardzewski definition of the Palm probability as a Radon-Nikodym derivative, which, in a stationary context, is equivalent to the Mecke definition.

We consider a stochastic fluid network with independent subordinator inputs to the various stations and deterministic internal flow which is of feed-forward type. We show that under suitable conditions the process of fluid contents in the station has a limiting distribution, where the limit holds in total variation and is independent of the initial condition. We also show that this limiting distribution is of product form only for trivial setups.

This paper considers a class of epidemic models in which susceptibles may enter or leave the population according to a general continuous time density dependent Markov chain. A sequence of such epidemics indexed by N, the initial number of susceptibles, is constructed on the same probability space as a time-inhomogeneous birth-and-death process. A coupling argument is then used to demonstrate the strong convergence of the sequence of infectives to the birth-and-death process. This result is used to provide a threshold analysis of the epidemic model in question.

We examine the existence of limiting behavior, or stability, for storage models with shot noise input and general release rules. The shot noise feature of the input process allows the individual inputs to gradually enter the store.

We first show that a store under the unit release rule is stable if and only if the traffic intensity is less than one; this extends the classic result of Prabhu (1980) to the case of shot noise input. The stability of the unit release rule store and various stochastic orderings are then used to derive a sufficient condition for a store with a general release rule to be stable. Finally, we show that when restricted to a compact state space, our storage model is always stable.

An important component of the paper is the methodology employed: coupling and stochastic monotonicity play a key role in analyzing the non-Markov processes encountered.