Refine listing
Actions for selected content:
1446 results in 60Kxx
An elementary renewal theorem for random compact convex sets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 931-942
- Print publication:
- December 1995
-
- Article
- Export citation
An algorithm to compute blocking probabilities in multi-rate multi-class multi-resource loss models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1104-1143
- Print publication:
- December 1995
-
- Article
- Export citation
A monotonicity result for a single-server queue subject to a Markov-modulated Poisson process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1103-1111
- Print publication:
- December 1995
-
- Article
- Export citation
Likelihood ratio gradient estimation for stochastic recursions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1019-1053
- Print publication:
- December 1995
-
- Article
- Export citation
A monotonicity result for a single-server loss system
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1112-1117
- Print publication:
- December 1995
-
- Article
- Export citation
Markov population replacement processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 711-740
- Print publication:
- September 1995
-
- Article
- Export citation
Some general characteristics of two-state reliability models for maintained systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 805-820
- Print publication:
- September 1995
-
- Article
- Export citation
Analysis of Markov renewal shock models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 821-831
- Print publication:
- September 1995
-
- Article
- Export citation
On almost optimal priority rules for preemptive scheduling of stochastic jobs on parallel machines
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 821-839
- Print publication:
- September 1995
-
- Article
- Export citation
Probability metrics and recursive algorithms
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 770-799
- Print publication:
- September 1995
-
- Article
- Export citation
On the estimation of probabilities for birth and death processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 623-634
- Print publication:
- September 1995
-
- Article
- Export citation
Analysis of an M/G/1 queue with two types of impatient units
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 840-861
- Print publication:
- September 1995
-
- Article
- Export citation
On unbounded hazard rates for smoothed perturbation analysis
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 659-667
- Print publication:
- September 1995
-
- Article
- Export citation
Ruin probabilities via local adjustment coefficients
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 736-755
- Print publication:
- September 1995
-
- Article
- Export citation
Event coupling and performance sensitivity analysis of generalized semi-Markov processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 741-769
- Print publication:
- September 1995
-
- Article
- Export citation
The probability of large queue lengths and waiting times in a heterogeneous multiserver queue I: Tight limits
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 532-566
- Print publication:
- June 1995
-
- Article
- Export citation
Limiting behavior of some measures of system availability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 482-493
- Print publication:
- June 1995
-
- Article
- Export citation
On M/G/1 queues with exhaustive service and generalized vacations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 510-531
- Print publication:
- June 1995
-
- Article
- Export citation
The probability of large queue lengths and waiting times in a heterogeneous multiserver queue II: Positive recurrence and logarithmic limits
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 567-583
- Print publication:
- June 1995
-
- Article
- Export citation
Darwin's log: a toy model of speciation and extinction
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 279-295
- Print publication:
- June 1995
-
- Article
- Export citation
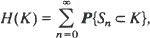
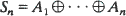 are Minkowski (element-wise) sums of i.i.d. random compact convex sets. In this paper we determine the limit of
are Minkowski (element-wise) sums of i.i.d. random compact convex sets. In this paper we determine the limit of 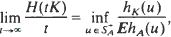
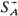 is the set of all unit vectors
is the set of all unit vectors 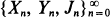 is considered, describing a sequence of random shocks {
is considered, describing a sequence of random shocks {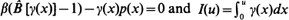 . It is shown that
. It is shown that 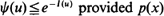 is non-decreasing and that log ψ(u) ≈ –
is non-decreasing and that log ψ(u) ≈ –